Centroid, Incentre, Orthocentre?
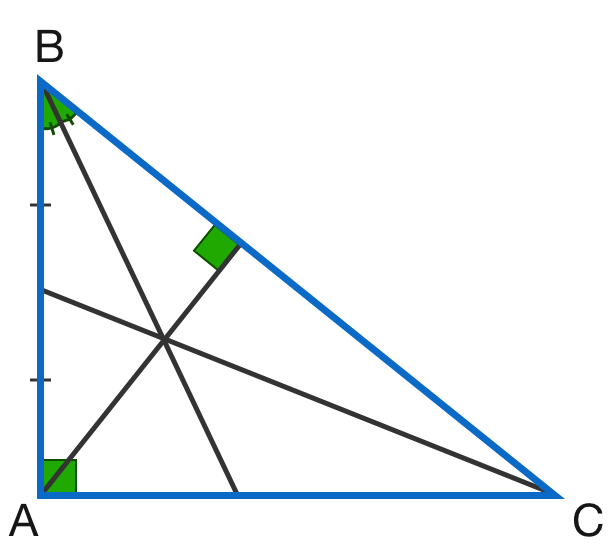
As shown above, an angle bisector, median, and altitude intersect at the same point in right triangle A B C .
cos 2 ∠ A B C = q + r p , where p and q are positive integers and r is a prime number . Find the value of p + q + r .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Rightly featured. Brilliant.
add diagram to illustrate where the point F is
My answer would have been same as Chan Lye Lee's but sir ur answer is brilliant I should have thought more
Sorry Mr Deeparaj Bhat , I don't review your solution before submitting my private.
good solution prof Ahmed i hope you well we have problem how can we put it in this site
Log in to reply
After you putting correct answer , click on discuss solution or no solution yet.
Page will open to writing and posting your detailed solution.
That's alright!
Relevant wiki: 2D Coordinate Geometry - Problem Solving
Let
A
=
(
0
,
0
)
,
B
=
(
0
,
2
p
)
,
C
=
(
2
q
,
0
)
and
F
=
(
r
,
0
)
. Then
E
=
(
0
,
p
)
.
Now the gradient of B C is − q p and the gradient of C E is − 2 q p . This means that the equation of A D is p y = q x and the equation of C E is y = − 2 q p x + p . Solving these equation, we get the intersect point G = ( p 2 + 2 q 2 2 p 2 q , p 2 + 2 q 2 2 p q 2 ) .
Next, since B F bisects ∠ A B C , 2 p 2 + q 2 2 p = 2 q − r r , which implies that r = p + p 2 + q 2 2 p q .
Since the points B , G and F collinear, the gradient of B F equals to the gradient of B G , which means that p + p 2 + q 2 2 p q − 2 p = p 2 + 2 q 2 2 p 2 q p 2 + 2 q 2 2 p q 2 − 2 p . After manipulation, we obtained q 2 = 2 1 + 5 p 2 .
Finally, cos 2 α = p 2 + q 2 p 2 = p 2 + 2 1 + 5 p 2 p 2 = 3 + 5 2 = b + c a . So a + b + c = 1 0 , as c is prime.
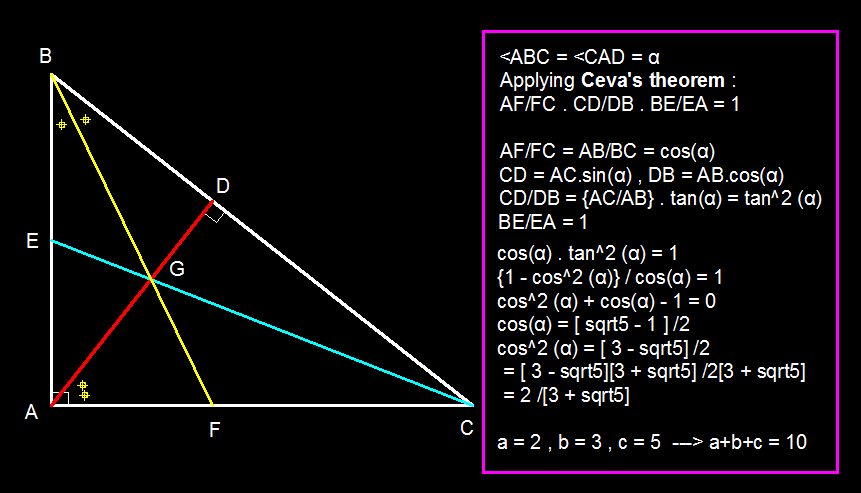
We shall use Ceva's theorem to convert the concurrency condition into an equivalent condition involving ratio of side lengths.
Referring to the figure, Ceva's theorem gives us F C A F ⋅ D B C D ⋅ E A B E = 1
Using the angle bisector theorem we have that F C A F = cos α
Using the definition of a median , we have E A B E = 1
Now, using a little trigonometry, we get the folowing:
B C A B A B B D ⟹ B D ⟹ C D ⟹ D B C D = cos α = cos α = B C cos 2 α = B C sin 2 α = tan 2 α
So, plugging all these into the first equation, we have:
cos α tan 2 α ⟹ tan 2 α ⟹ sec 2 α ⟹ sec α = 1 = sec α = sec α + 1 = φ ( ∵ sec α ≥ 1 )
Where φ is the golden ratio .
Now, cos α ⟹ cos 2 α = φ 1 = φ 2 1 = 1 + φ 1 = 1 + 2 1 + 5 1 = 3 + 5 2
Therefore, a = 2 b = 3 c = 5 a + b + c = 1 0