Centroid locus
Let be a fixed circle with radius , and a fixed point on its circumference.
Consider the set of all triangles satisfying
- is one of the vertices of
- is the circumcircle of
- the inradius of is
An example of one such triangle is below:
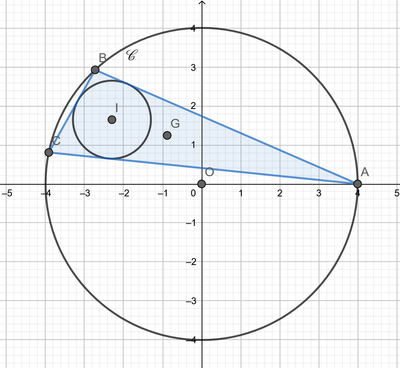
Find the locus of the centroids of all such triangles.
What is the length of ?
Bonus: find an equation for , and a "nice" expression for its length
Bonus bonus: does this curve have a name?
(among others)
The answer is 15.55673.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As I did this numerically, this is just a sketch solution. First of all, here's a picture of the locus: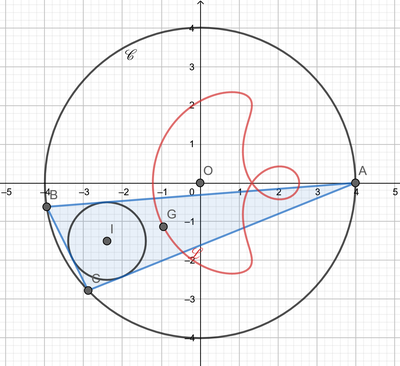
Some notation: O ( 0 , 0 ) is the circumcentre; I is the incentre; d = O I is the distance between them; G is the centroid; R = 4 and r = 1 are the circumradius and inradius. Let A ( R , 0 ) be the fixed vertex.
By Euler's theorem, O I 2 = R 2 − 2 R r so d is fixed and I lies on a circle of radius d centred at O . So we can parameterise the point I (and hence the triangles) by saying I ( d cos ( q ) , d sin ( q ) ) .
The aim is to calculate the coordinates of B and C in terms of q , so that we can find G .
Since we can now work out A I , we also get ∠ B A C = 2 sin − 1 A I r .
This is in fact enough; we know the gradient of the line A B , and that it goes through point A ; since O B = R we can work out the coordinates of B (and likewise C ) from this.
By tabulating the position of G for a high resolution of q values, we can work out the path length to be approximately 1 5 . 5 5 6 7 3 … .
This is messy, and (to me) quite unsatisfactory. For a deeper dive into this, we can use some other triangle formulas to find G .
We have G O 2 = 9 1 ( R 2 − a 2 − b 2 − c 2 ) and G A 2 = 9 1 ( 2 b 2 + 2 c 2 − a 2 ) , where a is as usual the length of the side opposite A , etc. We'll also use A to denote the angle ∠ B A C . Note that these are symmetric in lengths b and c - this is to be expected from the way they're defined.
By the extended sine rule, a = 2 R sin A .
Now consider the triangle B I C . By definition of the incentre, the altitude from I has length r . Also it's easy to show that ∠ B I C = 2 A + π . Using the fact the incentre lies on the angle bisectors, ∠ I B C = 2 B .
Combining all of this, B C = a = 2 R sin A = r ( cot 2 B + cot 2 C ) = r ( cot 2 B + tan 2 A + B )
This can be written as a quadratic in cot 2 B .
Ultimately, we can get expressions for b + c and b c , and from these work out b 2 + c 2 to get G O and G A . This gives a slightly neater way to work out the position of G ; but the expressions don't reduce very nicely. I'll post what I've found if anyone's interested, but I'd be really keen to see a less numerical solution.