Centroid of a conical frustrum
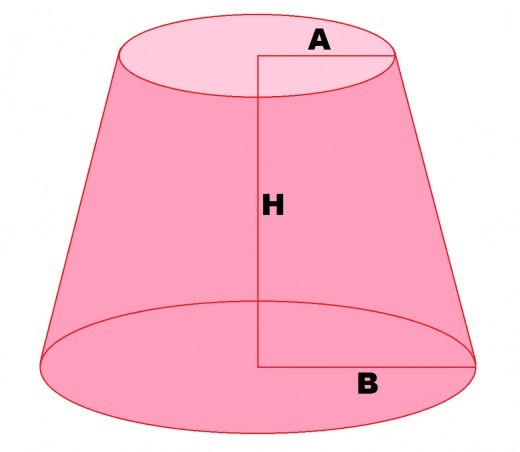
A conical frustrum (truncated cone) is shown in the above image. If the top radius and the bottom radius and the height , calculate how high above the bottom base is the centroid of the frustrum in centimeters.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The height of the centroid of the frustrum is Volume Weighted Mean = π ∫ 0 H ( B + ( A − B ) H x ) 2 d x π ∫ 0 H x ( B + ( A − B ) H x ) 2 d x = 3 1 π H ( A 2 + A B + B 2 ) 1 2 1 π H 2 ( 3 A 2 + 2 A B + B 2 ) = 4 ( A 2 + A B + B 2 ) H ( 3 A 2 + 2 A B + B 2 ) .
When A = 2 0 cm , B = 4 0 cm , and H = 2 8 cm , the height of the centroid is 4 ( 2 0 2 + 2 0 ⋅ 4 0 + 4 0 2 ) 2 8 ( 3 ( 2 0 ) 2 + 2 ⋅ 2 0 ⋅ 4 0 + 4 0 2 ) = 1 1 cm .