Centroid of a conical wedge

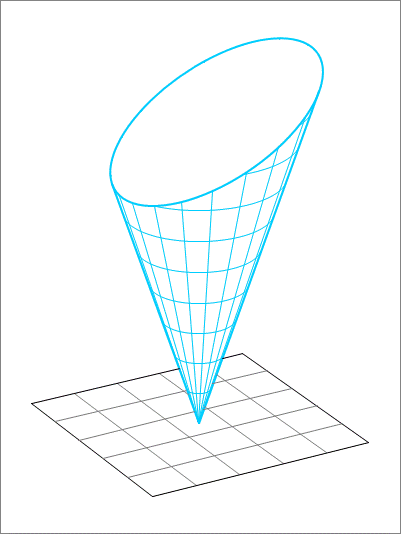Fig. 1 Right circular cone cut by a plane

A right circular solid cone with a semi-vertical angle of $\theta = \dfrac{\pi}{10}$ and its vertex at the origin opening in the positive $z$ axis direction is depicted in the figure above. The semi-vertical angle is defined as the angle between the axis of the cone and its surface. As shown in the figure, this solid cone is cut by the plane $z = z_0 + (\tan \phi) x$ , where $\phi = \dfrac{\pi}{6}$ , and $z_0 = 10$ . The figure depicts the part of the cone under this cutting plane. If the solid cone is made of a material of uniform density, find the centroid $G = (x, y, z)$ of this part of the cone, and submit the value of $\lfloor 200(x + z) \rfloor$ .

Details and Assumptions:

• You may need the following formulas for the semi-minor and semi-major axes lengths of the ellipse of intersection between the cone and the plane:

$\text{Semi-minor axis length } = a = \dfrac { z_0 \tan \theta \cos \phi}{\sqrt{1 - \sin^2 \phi \sec^2 \theta} }$

$\text{Semi-major axis length } = b = \dfrac { z_0 \tan \theta \cos \phi}{1 - \sin^2 \phi \sec^2 \theta}$

Where $z_0$ is the distance between the apex and the intersection point of the axis with the intercepting plane. $\theta$ is the semi-vertical angle of the cone, i.e. the angle between the axis of the cone and its surface. Finally, $\phi$ is the acute angle between the axis of the cone and the normal vector to the intersecting plane. And most importantly (actually this is the only formula you will need), the distance between the center of the ellipse and the point where the axis of the cone meets the cutting plane is given by $v_0$ ,

$v_0 = \dfrac{z_0 \sin \phi \tan^2 \theta}{1 - \sin^2 \phi \sec^2 \theta}$

These formulas were derived in the solution of this problem .