Centroid of a quarter-circular area
Geometry
Level
3
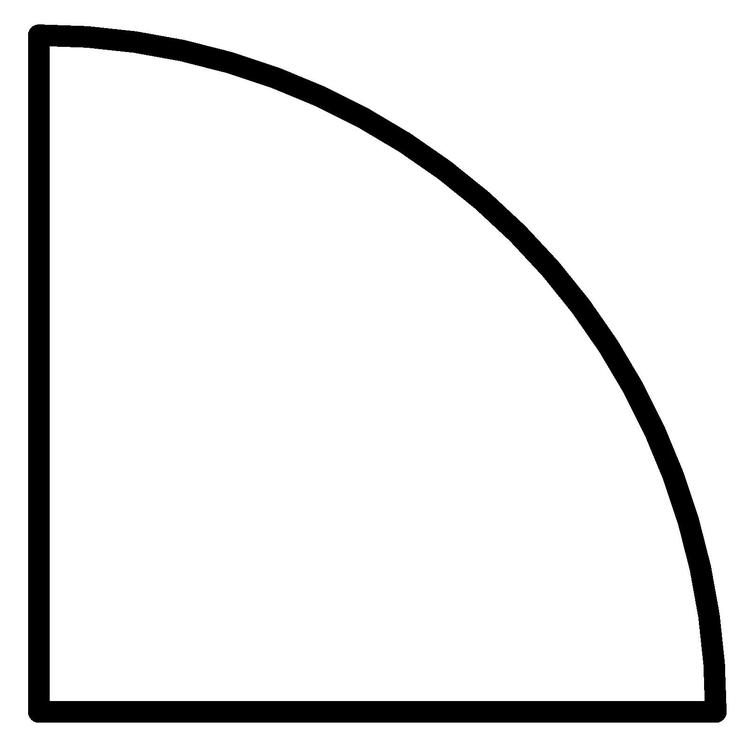Determine the centroid of a quarter-circular area of radius r. Consider a Cartesian axis with origin in the center of the circle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!