Centroid of half a pentagon - Number Crunching
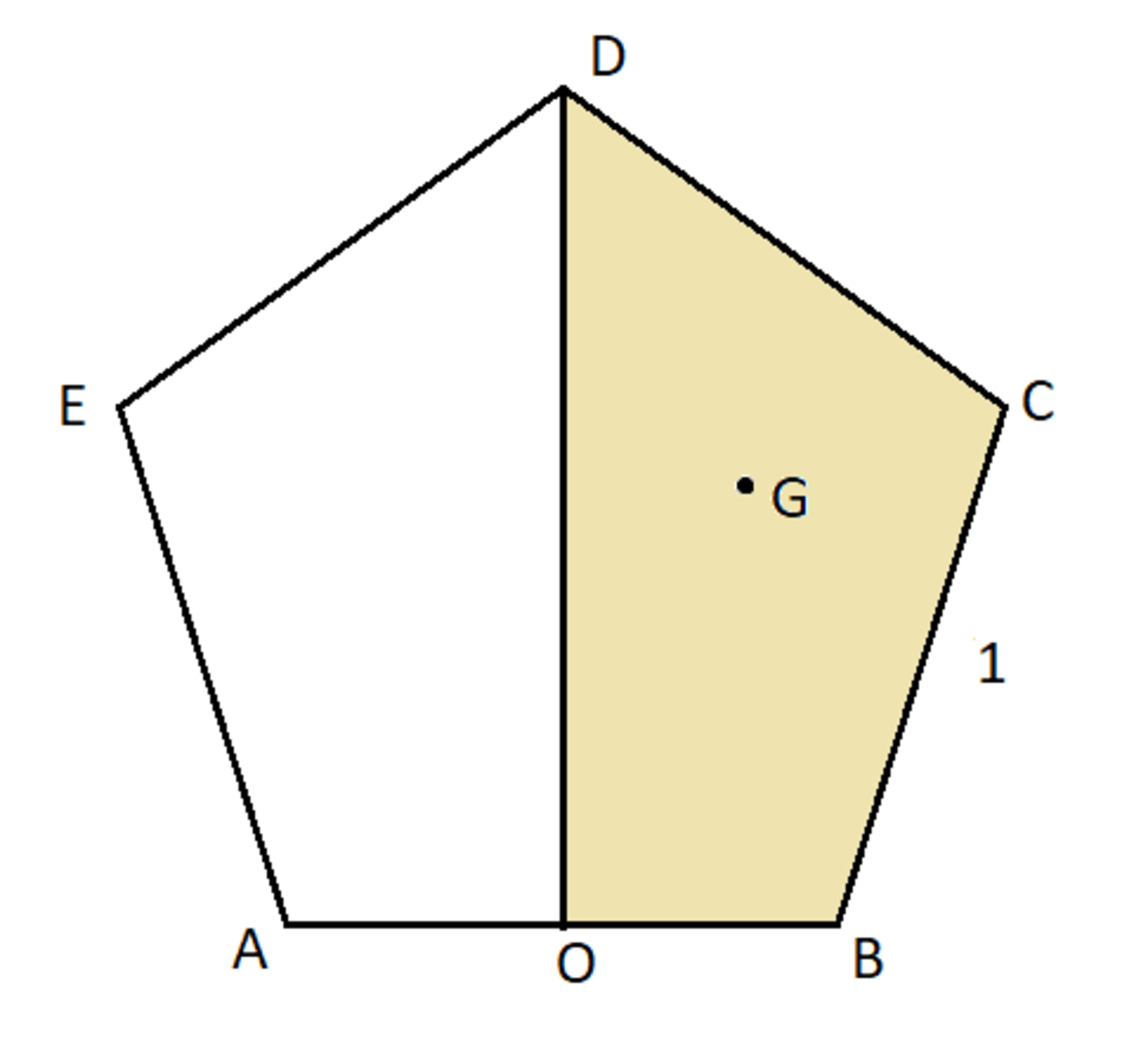
Shown in the figure above is a unit regular pentagon. It is divided into two halves by a vertical line that passes through the midpoint of the base (point ), which is the origin of the coordinate system. Find the coordinates of the centroid of the right half of the pentagon (shaded), and report the value of .
The answer is 3.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We have the following coordinates for points B , C , D :
B = ( 2 1 , 0 )
C = ( 2 1 + cos 7 2 ∘ , sin 7 2 ∘ )
D = ( 0 , sin 7 2 ∘ + sin 7 2 ∘ + 1 8 0 ∘ − 1 0 8 ∘ ) = ( 0 , sin 7 2 ∘ + sin 3 6 ∘ )
We'll segment the area of half the pentagon into two triangles, △ O B C and △ O C D ,
The centroid of △ O B C is given by
G 1 = ( 3 1 ) ( O + B + C )
And, the centroid of △ O C D is given by
G 2 = ( 3 1 ) ( O + C + D )
The overall centroid is given by
G = [ O B C ] + [ O C D ] [ O B C ] G 1 + [ O C D ] G 2
where, [ O B C ] is the area of △ O B C . [ O B C ] = 2 1 B x C y , and [ O C D ] is the area of △ O C D . [ O C D ] = 2 1 C x D y
Crunching the numbers above, we get G x = 0 . 3 1 5 7 3 7 8 6 5 , G y = 0 . 6 8 8 1 9 0 9 6 , so that 3 G x + 4 G y = 3 . 6 9 9 9 7 7 4 3 6 ≈ 3 . 7