Centroid Triangle

Let $D, E, F$ be the midpoints of $BC, CA, AB$ respectively.

Note that obviously $\dfrac{[DEF]}{[ABC]}=\dfrac{1}{4}$

Since $G_1$ is the centroid of $\triangle ABG$ , then $GG_1=2G_1F$

Similarly, $GG_2 = 2G_2D$ $GG_3 = 2G_3E$

Thus, $\triangle G_1G_2G_3$ maps to $\triangle FDE$ by a homothety of ratio $\dfrac{2}{3}$ .

Therefore, $\dfrac{[G_1G_2G_3]}{[DEF]} = \left(\dfrac{2}{3}\right)^2=\dfrac{4}{9}$

Finally, $\dfrac{[G_1G_2G_3]}{[ABC]} = \dfrac{[G_1G_2G_3]}{[DEF]}\cdot \dfrac{[DEF]}{[ABC]} = \dfrac{4}{9}\cdot \dfrac{1}{4}=\dfrac{1}{9}$ and our answer is $1+9=\boxed{10}$

We know that a centroid divides a median in ratio 2:1. Hence,

Let AD = x, BE = y, CF = z.

$GD = \frac{1}{3}x, GE = \frac{1}{3}y, GF = \frac{1}{3}z$

$G{G}_{1} = \frac{2}{9}x, G{G}_{2} = \frac{2}{9}y, G{G}_{3} = \frac{2}{9}z$

Now, $[{G}_{1}{G}_{2}{G}_{3}] = [G{G}_{1}{G}_{2}] + [G{G}_{1}{G}_{3}] + [G{G}_{2}{G}_{3}]$

$[G{G}_{1}{G}_{2}] = \frac{1}{2}*\frac{2}{9}x*\frac{2}{9}y*sin{\theta}_{1}$

$[G{G}_{1}{G}_{3}] = \frac{1}{2}*\frac{2}{9}y*\frac{2}{9}z*sin{\theta}_{2}$

$[G{G}_{2}{G}_{3}] = \frac{1}{2}*\frac{2}{9}z*\frac{2}{9}x*sin{\theta}_{3}$

if ${\theta}_{1}, {\theta}_{2}, {\theta}_{3}$ are angles ${G}_{1}G{G}_{2}, {G}_{1}G{G}_{3}, {G}_{2}G{G}_{3}$ respectively.

Similarly, $[ABC] = \frac{1}{2}*\frac{2}{3}*\frac{2}{3}(xysin{\theta}_{1} + yzsin{\theta}_{2} + zxsin{\theta}_{3})$

As a result, $[{G}_{1}{G}_{2}{G}_{3}]:[ABC] = \frac{\frac{1}{2}*\frac{2}{9}*\frac{2}{9}(xysin{\theta}_{1} + yzsin{\theta}_{2} + zxsin{\theta}_{3})}{\frac{1}{2}*\frac{2}{3}*\frac{2}{3}(xysin{\theta}_{1} + yzsin{\theta}_{2} + zxsin{\theta}_{3})}$

$=1:9$

So, $p + q = \boxed{10}$

It does not reduce generalization, assume ABC is a equilateral triangle. So: $\frac{G_1G_3}{IK}=\frac{2}{3}$ $\frac{G_1G_3}{BC}=\frac{2}{3} \times \frac{1}{2}=\frac{1}{3}$ $\frac{[G_1G_2G_3]}{[ABC]}=\frac{1}{9} \Rightarrow p+q=\boxed{10}$

First, let's extend $AG, BG$ and $CG$ to meet $\triangle ABC$ at $E, D$ and $F$ respectively. Since each median of the larger triangle bisects the side of one of the smaller triangles, we can say that $(A, G_2)$ , $(C,G_1)$ and $(B, G_3)$ are collinear. Also, note that $G_1G_3 || BC$ by midpoint theorem.

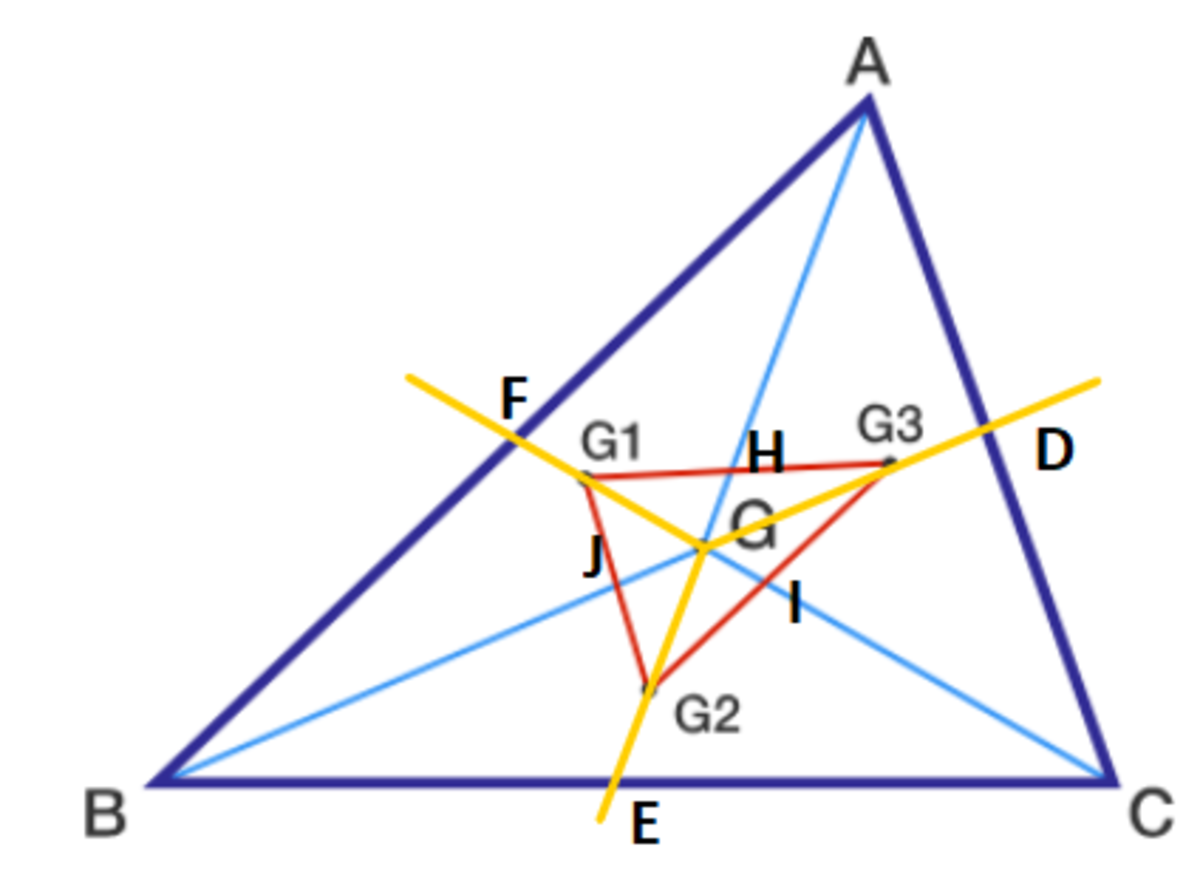
Therefore, $\angle BGE = \angle HGG_3$ and $\angle BEG = \angle G_3HG$ $\Rightarrow \triangle GEB \approx \triangle GHG_3$ . Now, we know that $\frac {BG}{2} = GD$ and $\frac {2}{3}GD = GG_3$ . So, $\frac {BG}{3} = GG_3$ . Which implies -

$s_1 = 3s_2 . . . . . . . . . . . .. . . . .. (1)$

(Where $s_1$ is the semiperimeter of $\triangle GEB$ and $s_2$ is the semiperimeter of $\triangle GHG_3$ ).

By the law of cotangents $r_1 = \frac {3s - 3GH}{\cot \frac {\angle GBE}{2}}$ and $r_2 = \frac {s - GH}{\cot \frac {\angle GG_3H}{2}}$ .

(Where $r_1$ is the inradius of $\triangle GEB$ and $r_2$ is the inradius of $\triangle GHG_3$ ). Which gives us -

$r_1 = 3r_2 . . . . . . . . .. . . (2)$ .

Using the formula $[ABC]$ = inradius $\cdot$ semiperimeter, we can say from $(1)$ and $(2)$ that -

$9[GHG_3] = [GEB]$ . Observe that $G$ is the centroid of $\triangle G_1G_2G_3$ .It can also be proven that the medians and centriod of a triangle divide it into six triangles of equal area (but not necessarily congruent ones).

So we can conclude that, $\frac {[G_1G_2G_3]}{[ABC]} = \frac {1}{9} \Rightarrow p + q = \boxed {10}$

Note - because $\triangle BEG \approx \triangle GHG_3, \triangle GEC \approx \triangle GHG_1$ and $BE = CE$ , we also proved that $G$ is the centroid of $G_1G_2G_3$ .

Let M be the midpoint of BG,we get $\frac{G_1M}{MA}$ = $\frac{1}{3}$ and $\frac{G_2M}{CM}$ = $\frac{1}{3}$ so we get $\frac{G_2G_1}{AC}$ = $\frac{1}{3}$ by the same approach each side of $\ triangle G_1G_2G_3$ is one-third of its corresponding side in ABC so the area is one-ninth so p+q=10