Cevian in Isosceles Right Triangle
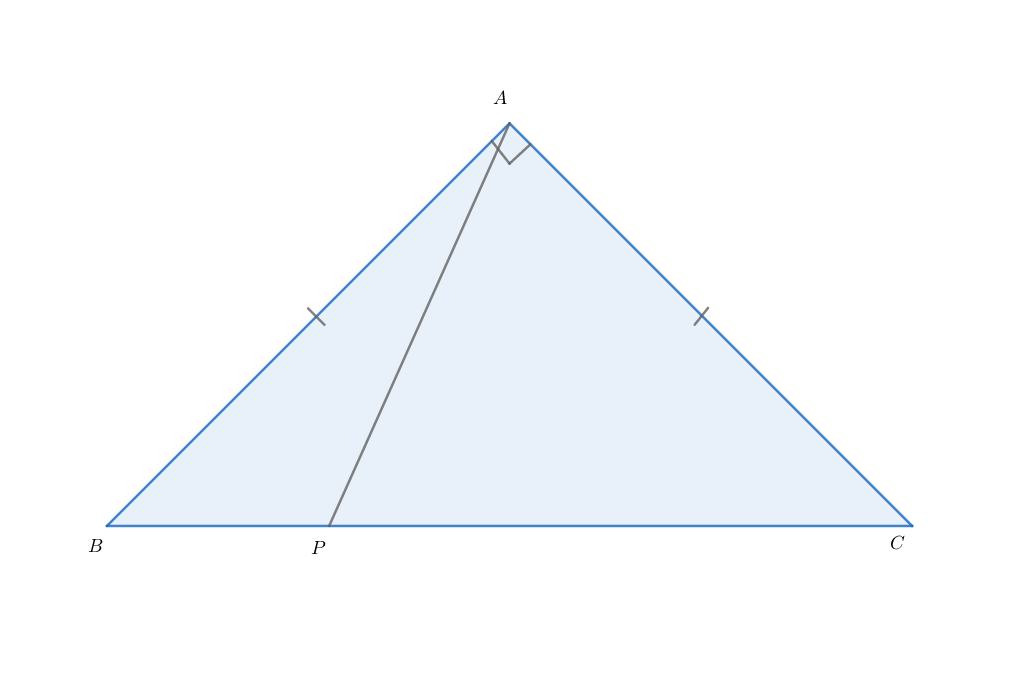
In , and
is a point on with and .
Find the length of rounded to the rd decimal place.
Bonus : Generalize this for general value of and with is any point between and .
The answer is 8.062.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Stewart's theorem states (with relation to the given triangle) that
( A B ) 2 P C + ( A C ) 2 P B = B C ( ( P B ) ( P C ) + ( P A ) 2 )
Given the quantities P B = 3 and P C = 1 1 , we have that B C = 1 4 and since the triangle A B C is an isosceles right triangle, we also have that A B = A C = 2 1 4 . Substituting the required quantities into the statement of Stewart's theorem, we have the following:
1 4 ( 2 1 4 ) 2 = 1 4 ( 3 3 + ( P A ) 2 )
Dividing both sides by 1 4 and computing that ( 2 1 4 ) 2 = 2 1 9 6 = 9 8 , we have that
( P A ) 2 = 6 5 ,
meaninig that P A = 6 5 . Round off the answer as you may (that's if you believe in any of the square root jargon).
P.S. I have looked at a reformulation of Stewart's theorem using only the framework of Rational trigonometry; view my video and Wildberger's at the following links given.