Cevius Maximus
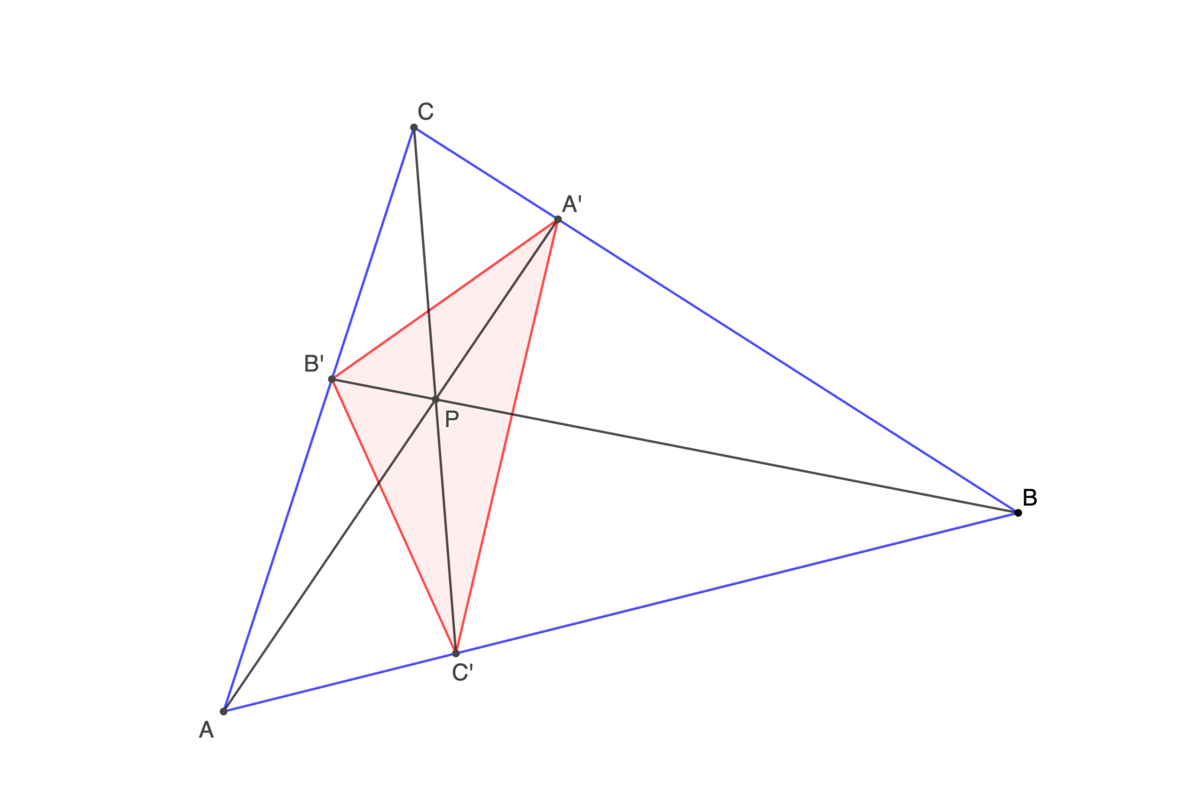
is an arbitrary point in which is used to construct a cevian triangle , . Find the maximum ratio, , express it as , where and are coprime integers, and submit .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since stretching a triangle preserves ratios of areas, stretch the triangle so that the vertices are at A ( 0 , 0 ) , B ( 1 2 , 0 ) , C ( 0 , 1 2 ) , and P ( p , q ) .
A A ′ has the equation y = p q x , and intersects B C or y = 1 2 − x at A ′ ( p + q 1 2 p , p + q 1 2 q ) .
B B ′ has the equation y = p − 1 2 q ( x − 1 2 ) , and has a y -intercept of B ′ ( 0 , 1 2 − p 1 2 q ) .
C C ′ has the equation y = p q − 1 2 x + 1 2 , and has an x -intercept of C ′ ( 1 2 − q 1 2 p , 0 ) .
A ′ B ′ = ( − p + q 1 2 p , 1 2 − p 1 2 q − p + q 1 2 q ) and A ′ C ′ = ( 1 2 − q 1 2 q − p + q 1 2 p , − p + q 1 2 q ) .
The area of △ A ′ B ′ C ′ is A △ A ′ B ′ C ′ = 2 1 ∣ A ′ B ′ x ⋅ A ′ C ′ y − A ′ B ′ y ⋅ A ′ C ′ x ∣ = ( 1 2 − p ) ( 1 2 − q ) ( p + q ) 1 4 4 p q ( 1 2 − p − q ) .
The maximum area of △ A ′ B ′ C ′ occurs when d p d A △ A ′ B ′ C ′ = ( 1 2 − p ) 2 ( 1 2 − q ) ( p + q ) 2 1 7 2 8 q 2 ( 1 2 − 2 p − q ) = 0 and d q d A △ A ′ B ′ C ′ = ( 1 2 − p ) ( 1 2 − q ) 2 ( p + q ) 2 1 7 2 8 p 2 ( 1 2 − p − 2 q ) = 0 .
For p = 0 and q = 0 , this means that 1 2 − 2 p − q = 0 and 1 2 − p − 2 q = 0 , which solves to p = q = 4 (the centroid) and makes the maximum area A △ A ′ B ′ C ′ max = ( 1 2 − 4 ) ( 1 2 − 4 ) ( 4 + 4 ) 1 4 4 ⋅ 4 ⋅ 4 ⋅ ( 1 2 − 4 − 4 ) = 1 8 .
Therefore, since the area of △ A B C is A △ A B C = 2 1 ⋅ 1 2 ⋅ 1 2 = 7 2 , the maximum ratio is A △ A B C A △ A ′ B ′ C ′ max = 7 2 1 8 = 4 1 , so p = 1 , q = 4 , and p + q = 5 .