Chain! Not again!
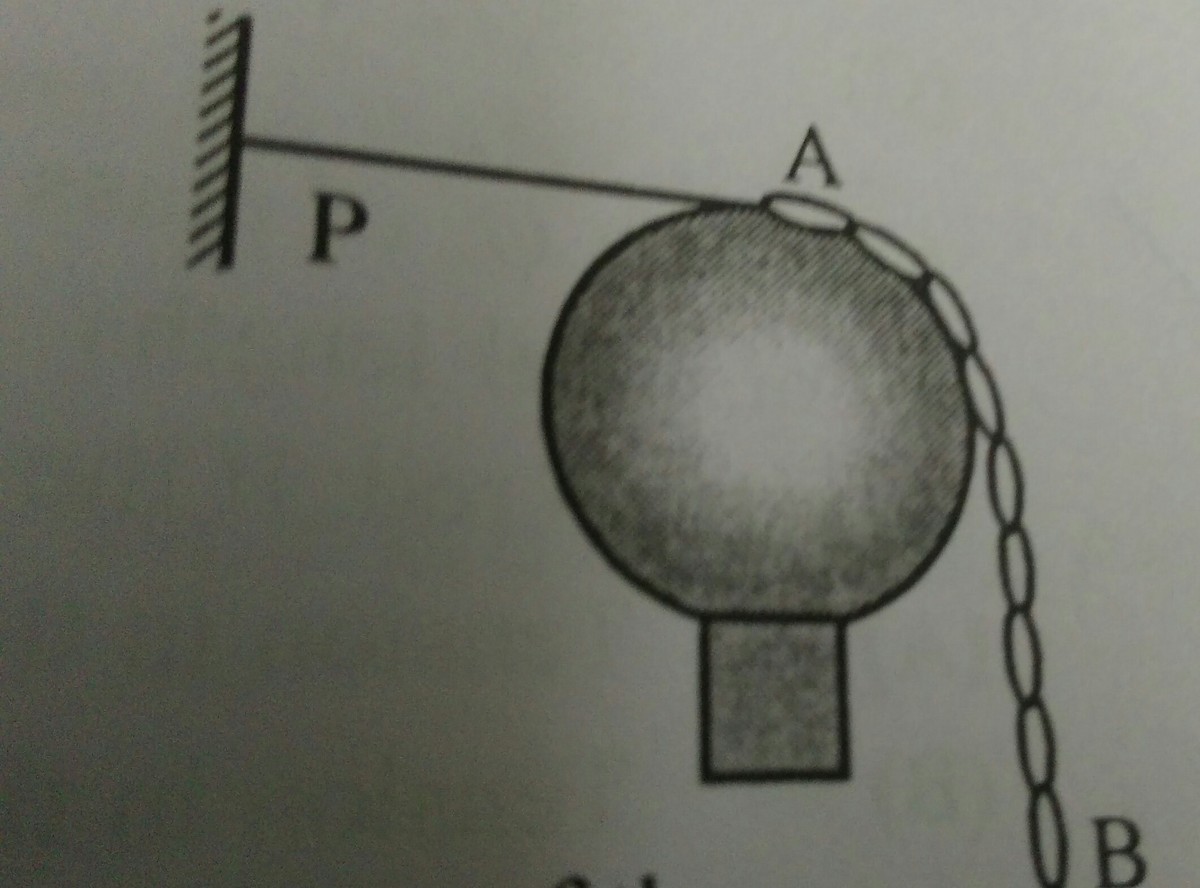
A chain of mass per unit length ¥ and length 1.5m rests on a fixed smooth sphere off radius R=2/π metre such that“A” end of a chain is at top of the sphere while the other end is hanging freely . Chain is held stationary by a horizontal thread PA. The tension in the thread is:
Fig:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The portion in contact with the sphere is 2 ∗ π ∗ R ∗ 4 1 = 2 ∗ π ∗ π 2 ∗ 4 1 = 1 m . During this, the chain losses a hight of R m = π 2 m ∴ h a n g i n g p o r t i o n = 1 . 5 − 1 = 2 1 . So the total tension is Y ( π 2 + 2 1 . )