Challenges in Mechanics by Ronak Agarwal (Part 4)

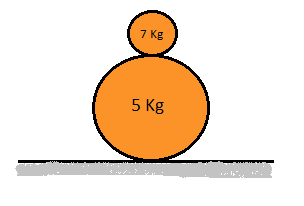
On a smooth ground a rough sphere of mass ${m}_{1}$ and radius ${r}_{1}$ is placed. On this big sphere a small sphere of mass ${m}_{2}$ and radius ${r}_{2}$ is placed right at the top as shown in the figure. The system is in unstable equilibrium. Now the equilibrium is disturbed by giving a slight push to the upper sphere.

Now if the upper sphere makes an angle $\theta$ with the vertical when it leaves contact with the lower sphere then $\cos(\theta) = \dfrac{a}{b}$ , find $a+b$

Details and Assumptions :

1) There is no friction between ground and the lower sphere.Assume sufficient friction between the two sphere's at all times. ( This assumption may seem a little incorrect since one may argue that as normal is tending to zero there must come a point where friction is insufficient for a finite co-efficient of friction, so you can assume infinite co-efficient of friction)

2) ${m}_{1} = 5 \text{Kg} , {m}_{2} = 7 \text{Kg}, {r}_{1} = 3 \text{m} , {r}_{2} = 1 \text{m}, g=10 m/{s}^{2}$

3) The sphere's are solid spheres.

4) $a,b$ are positive co-prime integers less than $20$ .

---

My series of problem Challenges in Mechanics( although only three problems) got quite famous hence I decided it to extend it. hence the fourth part of this series.

Part 1

Part 2

Part 3