Challenging
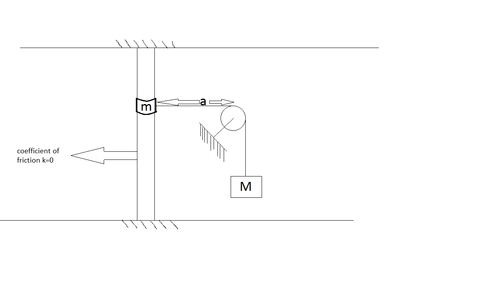A ring of mass
slides on a smooth vertical rod. A light string is attached to the ring and is passing over a smooth pulley over a smooth peg at a distance
from the rod, and at the other end of the string is a mass
. The ring is held on a level with the peg and released. What is the distance traveled before it comes to rest for first time?
Assumptions and Details
- kg
- kg
- m
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This can be solved by the conservation of energy. The ring will be in the rest position when loss in potential energy of ring is equal to the gain the potential energy of the the block.
Let the distance traveled by the ring before it comes to rest be x
Loss in the potential energy of ring is m g x
When the ring falls down by the distance x then the length of string to the right of the pulley will increase by length a 2 + x 2 − a . As the length of the string is constant so the by the same distance block M will move up.
So m g x = M g ( a 2 + x 2 − a )
On putting values we get x = 4 m