Challenging Coordinates Calculation

Geometry Level pending

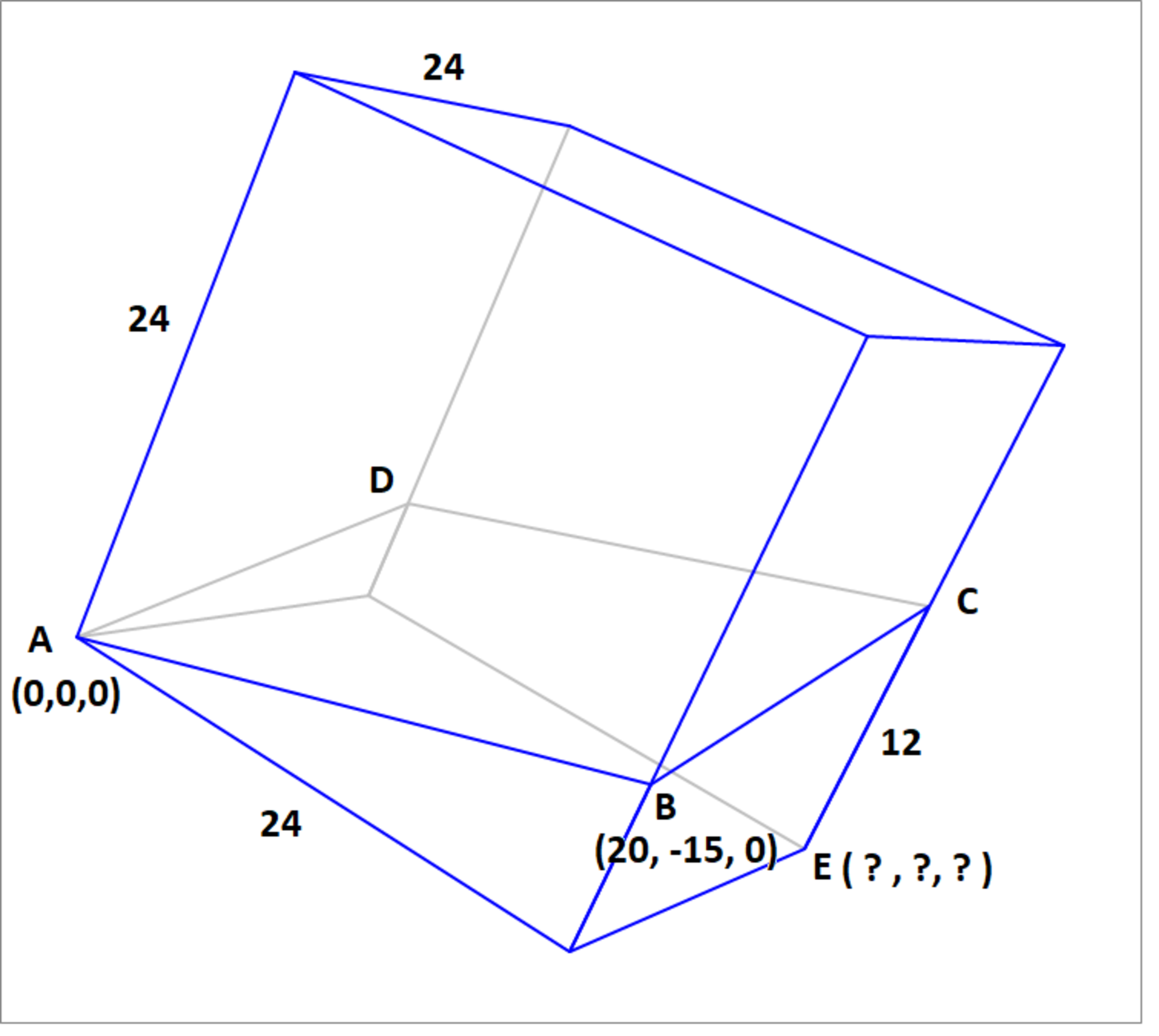
A cube has an edge length of $24$ units. It is tilted and rotated about one of its base vertices (vertex A), such that its four parallel edges that were vertical intersect the horizontal $xy$ plane passing through vertex A, at the points A, B, C and D. If the coordinates of point B are $(20, -15, 0)$ , and point C is $12$ units away from the base. What are the coordinates $(x,y,z)$ of the lowest point of the cube (vertex E)? As your answer, submit the sum of these coordinates $(x + y + z)$ .

The answer is 24.414.

1 solution

Steven Chase
Dec 16, 2018

Setup (given $\theta$ and $\phi$ ):

$L = 24 \\ F_x = L \, cos \theta \, sin \phi \\ F_y = L \, sin \theta \, sin \phi \\ F_z = L \, cos \phi \\ \vec{v_1} = \vec{F} - \vec{A} \\ \vec{v_2} = \vec{B} - \vec{F} \\ \vec{u_1} = \vec{v_1} / |\vec{v_1} | \\ \vec{u_2} = \vec{v_2} / |\vec{v_2} | \\ \vec{u_3} = \vec{u_2 } \times \vec{u_1} \\ \vec{v_3} = L \, \vec{u_3} \\ \vec{E} = \vec{F} + \vec{v_3} \\ \vec{C} = \vec{E} + \frac{L}{2} \, \vec{u_2}$

Using a numerical solution, find $\theta$ and $\phi$ such that the following are true. Expressions for coordinates of $\vec{E}$ are as shown above. $\vec{E} \approx (31.7616,3.9488,-11.2963)$

$\vec{u_1} \cdot \vec{u_2} = 0 \\ C_z = 0$

Challenging Coordinates Calculation

The answer is 24.414.

1 solution

0 pending reports