Challenging Electricity Problem!
Level
2
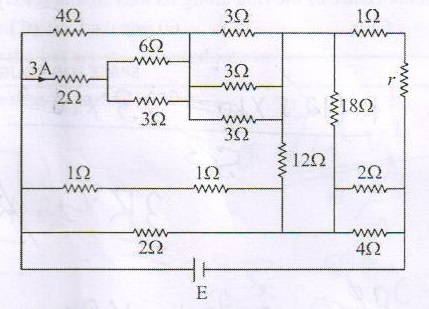 The current through 12 ohm resistance is zero. The value of E is:
The current through 12 ohm resistance is zero. The value of E is:
42V
36V
24V
45V
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Resistors with no current to flow are having potential difference of 0 V and therefore can be detached from the circuit. This simplify the whole circuit into resultant resistances of:
(3 Ω ~ 1 Ω ~ r Ω ) // (1 Ω ~ 3 4 Ω )
Further simplified into:
(4 Ω ~ r Ω ) // ( 3 7 Ω )
Voltage across 2 Ω resistor with 3 A is 6 V. Another resultant resistance of 2 Ω in series with it formed from 3 Ω // 6 Ω is also 6 V. Therefore, voltage across 4 Ω resistor is 12 V.Since 4 Ω , 2 Ω , 6 Ω and 3 Ω resulted with 2 Ω , in series with 3 Ω , 3 Ω and 3 Ω in parallel of 1 Ω as resultant resistance, voltage across (1 Ω ~ 1 Ω ) // 2 Ω is therefore 18 V.
For semi-resultant of (3 Ω ~ 1 Ω ~ r Ω ) // (1 Ω ~ 3 4 Ω ), total current through the 2nd 1 Ω resistor is therefore 18 A.
To (4 Ω ~ r Ω ) // ( 3 7 Ω ), the later is having voltage of 3 7 Ω × 1 8 A = 4 2 V
Note that r = 3 Ω as 42 V - 4 Ω × 6 A = 18 V, and therefore 6 A 1 8 V = 3 Ω . The whole circuit draws an amount of 24 A which is a high loading to usual batteries. The batteries must be high power batteries to be able to give a voltage required.
Voltage across the batteries or cell, E = 42 V
Answer: 4 2