A geometry problem by Shamin Yeaser
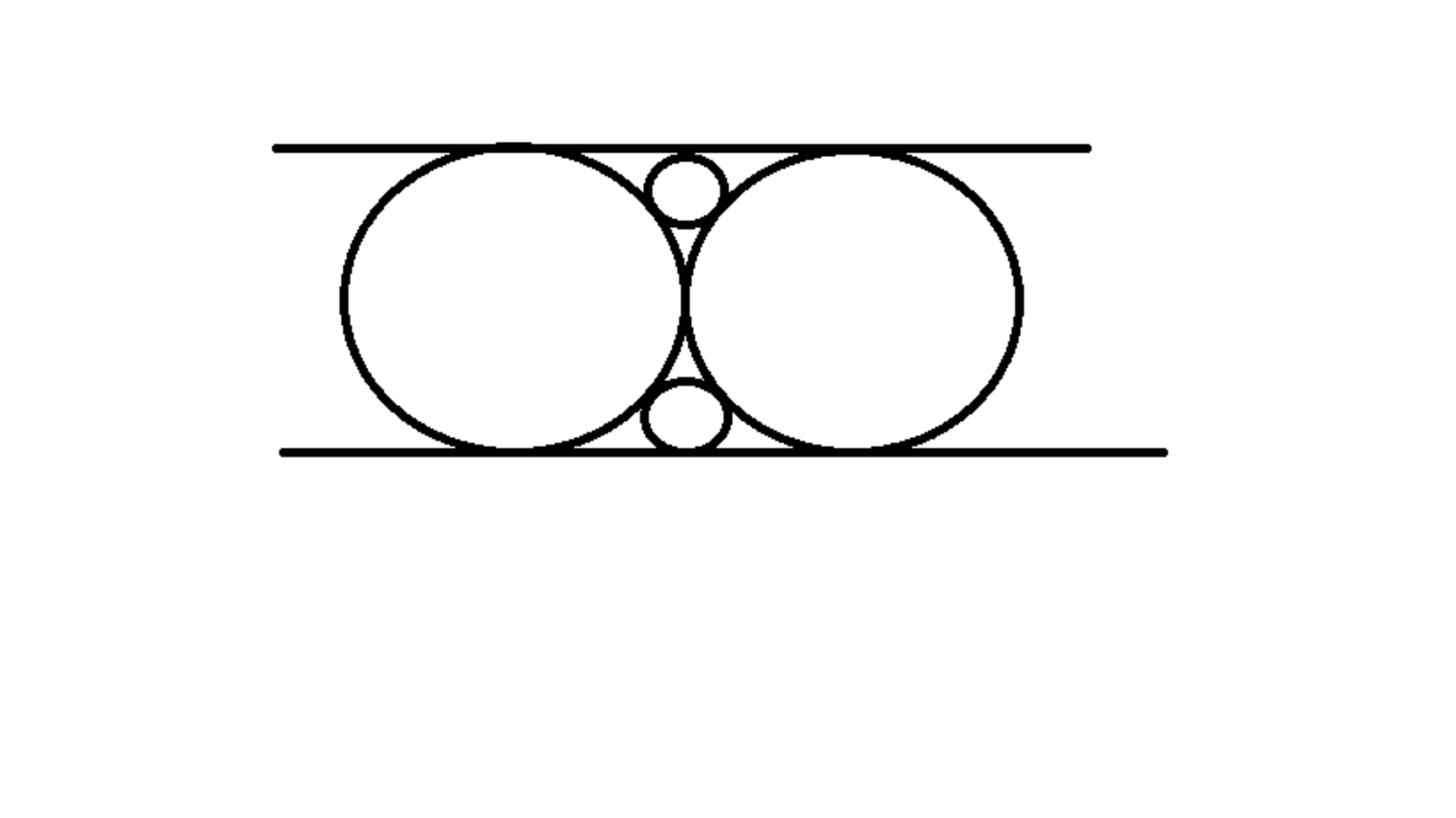
In the figure, if the distance between the centers of the two small circles is 90, what will be the diameter of the two identical large circles? [NOTE:the two lines are parallel and the small circles and the bigger circles have same radius separately]
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
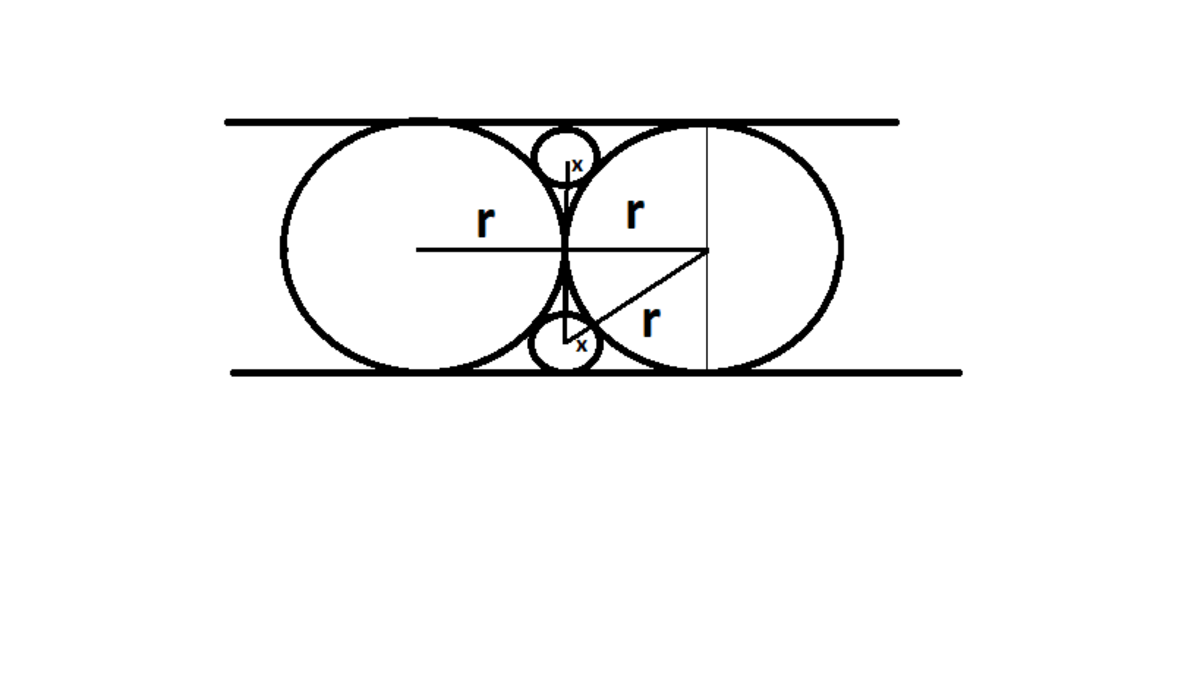
1) Use the above result to obtain the relationship between the radius of the smaller circle (r) and the larger circle (R) as R = 4r
2) Next use Pythagoras theorem to obtain the result (R+ r)^2 - R^2 = (90/2)^2 = 45^2
Solve for R and find 2R. ( R = 60 and r = 15)