Challenging Geometry Reasoning
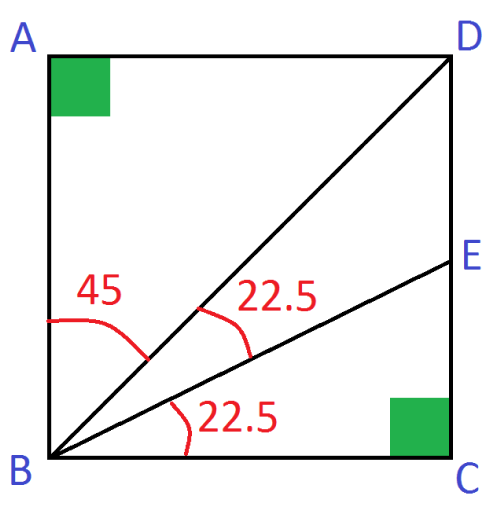 In the diagram above,
A
B
C
D
is a square.
B
D
is the angle bisector of
∠
A
B
C
and
B
E
is the angle bisector of
∠
D
B
C
.
In the diagram above,
A
B
C
D
is a square.
B
D
is the angle bisector of
∠
A
B
C
and
B
E
is the angle bisector of
∠
D
B
C
.
Find E C in terms of D E .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
You can apply the angle bisector theorem directly, to see that
D E E C = B D B C = 2 1 .
Nice solution
LOL i used trigonometry and derive tan22.5° by formula trignometric functions....

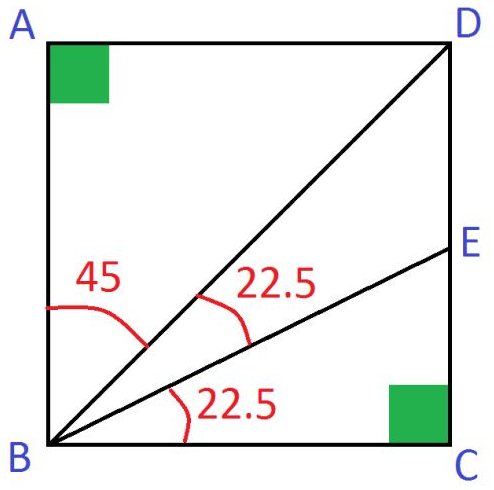

[invalid file: https://d18l82el6cdm1i.cloudfront.net/uploads/GbJrKlf6XI-zxc.png]
Find point F on line BD such that it forms a right triangle DFE. The rest follows, as FE = EC.
tan 22.5 = sqrt(2)-1 Thus, tan22.5= EC/BC Thus, BC = EC/(sqrt(2)-1) Also, tan 45 =1 and thus, DC = BC = DE + EC Thus, DE+EC = EC/(sqrt(2)-1) Thus sqrt(2)DE - DE + sqrt(2)EC-EC=EC. Thus, sqrt(2)EC(sqrt(2)-1)=DE(sqrt(2)-1). Thus, EC=1/sqrt(2) DE = sqrt(2)/2 DE
In △ B D E , ∠ B D E = 4 5 ∘ since B D is the angle bisecting line.
Using sine rule,
sin 2 2 . 5 D E = sin 4 5 B E ( 1 )
In △ B E C , ∠ B C E = 9 0 ∘ as it is the squares edge. (square property).
Using the sine rule here we obtain,
sin 2 2 . 5 E C = B E ( 2 )
Letting B E subject in ( 1 ) and ( 2 ) we attain,
B E = sin 2 2 . 5 sin 4 5 D E ( 1 ) B E = sin 2 2 . 5 E C ( 2 )
Thus BE = BE and we attain,
sin 2 2 . 5 sin 4 5 D E = sin 2 2 . 5 E C
Multiplying both sides by sin 2 2 . 5 we obtain, ( note that sin 4 5 = 2 2 ).
E C = 2 2 D E