Complexity Of Frame Changes

Classical Mechanics Level 5

A ring of radius $R$ is rolling without slipping on a horizontal surface at a linear speed of $v$ .

Let $P$ and $Q$ be two points on the ring, as shown in the figure above.

Find the radius of curvature of the path traveled by $P$ as observed from $Q$ .

Details and Assumptions:

Take $R = 10\text{ m}, v = 25 \text{ m/s},$ and $\theta = 30^{\circ}$ .

The answer is 5.176.

2 solutions

Xinghong Fu
Nov 24, 2016

The motion of the ring can be split into 2 parts- part 1 is the rotation about the center and part 2 is the translational speed of v. Since all points on the ring move at the same translational speed, transforming into the frame of any point on the ring would have no effect and part 2 is irrelevant to the problem. Now moving into Q's frame of reference, it is now simply the rotation of the ring about Q as shown in the diagram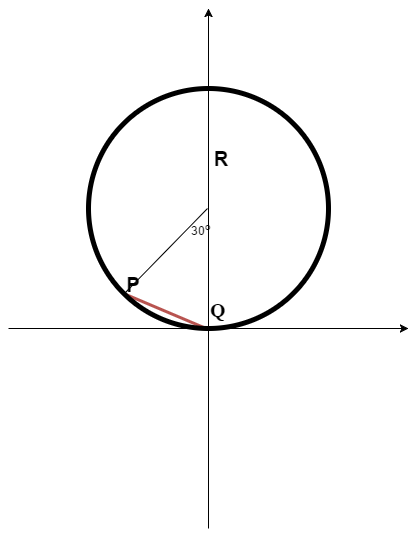

The red line will be the radius of curvature and it would be $2R \sin(15^o)=5.176$

I used the same logic to solve this problem.

Dhanvanth Balakrishnan - 4 years, 6 months ago

Steven Chase
Nov 11, 2016

The distance between P and Q is fixed, since they're both attached to the same ring. Taking Q as stationary (the frame of reference), any rotation of P must be circular at a radius of that PQ distance

Erich Enke - 4 years, 6 months ago

The observation system of Q is not sufficiently defined. If it is attached to the ring, Q observes no movement of P at all. If coordinate axes are assumed to be parallel to the fixed system axes, then Q observes a circular movement of P as nicely made clear by Erich Enke.

Jochem König - 4 years, 6 months ago

Actually,radius curvature of the path can be found by,first of all deriving the equation of radius in the functions- (1+(dy/dx)^2)^(3÷2)/y" and then the answer will be 108 or 109.

Emil Alizadeh - 4 years, 6 months ago

Complexity Of Frame Changes

The answer is 5.176.

2 solutions

0 pending reports