Change in Frequency of Charged Ball's!
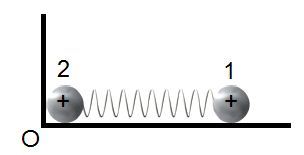 Two small identical balls lying on a horizontal plane are connected by a weightless spring. One Ball (
Ball 2
) is fixed at
and the other (
Ball 1
) is free. The balls are charged identically as a resultant of which the spring length increases
times. Determine the change in the frequency (ratio of
).
Two small identical balls lying on a horizontal plane are connected by a weightless spring. One Ball (
Ball 2
) is fixed at
and the other (
Ball 1
) is free. The balls are charged identically as a resultant of which the spring length increases
times. Determine the change in the frequency (ratio of
).
The answer is 1.4142.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When the balls are uncharged, frequency f 0 = 2 π 1 m k
When the balls are identically charged,
4 π ϵ 0 ( η l ) 2 q 2 = k ( η l − l ) . . . . . . . . . ( i )
(where l is the natural length of the spring and η l is the new length of the spring after extension.)
or l 3 = 4 π ϵ 0 η 2 ( η − 1 ) k q 2 . . . . . . . . . . . . ( i i )
When the ball 1 is displaced by a small distance x from the equilibrium position to the right, the unbalanced force to the right is given by
F r = 4 π ϵ 0 ( η l + x ) 2 q 2 − k ( η l + x − l )
Using Newton's law,
m d t 2 d 2 x = 4 π ϵ 0 1 η 2 l 2 q 2 ( 1 + η l x ) − 2 − k l ( η − 1 ) − k x
Now expanding binomially and using equations ( i ) & ( i i ) , we get
d t 2 d 2 x = − ( η 3 η − 2 ) m k x
Now use the definition of Simple Harmonic Motion
d t 2 d 2 x = − ω 2 x to find ω and thus, the new frequency f ′