Change it

Probability Level 2

You are in the final round of a competition!

The host presents you three boxes and indicates that one of those contains the prize. Then you are asked to pick a box out of three.

So you choose one of them. Now at least one of the remaning two boxes is empty.

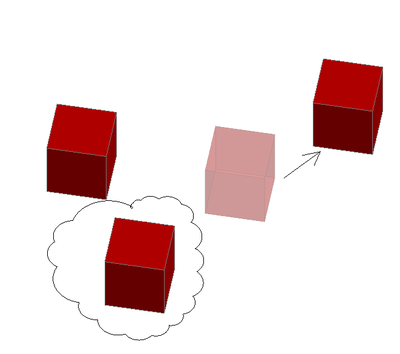
The host puts away one empty box from the remaing two boxes (since she knows which box contains the prize) Now you are given a chance to change your first choice!

What is the probablity of getting the prize if you change your first choice and choose the remaining box?

\frac{1}{3}

\frac{1}{2}

\frac{2}{3}

2 solutions

Parth Sankhe
Dec 11, 2018

The only way you could win if you switch is if you picked one of the empty ones at the start, which has a probability of $\frac {2}{3}$ .

Tolga Gürol
Dec 11, 2018

Think of "changing the box" as NOT operator. It converts losing to winning, and vica versa.

At the beginning the probablity of getting the prize is $\frac{1}{3}$ and in the end you will get the prize or not. If you change the box the probablity of getting the prize is $1-\frac{1}{3} = \boxed{\frac{2}{3}}$ .

Change it

2 solutions

0 pending reports