Changing Mass
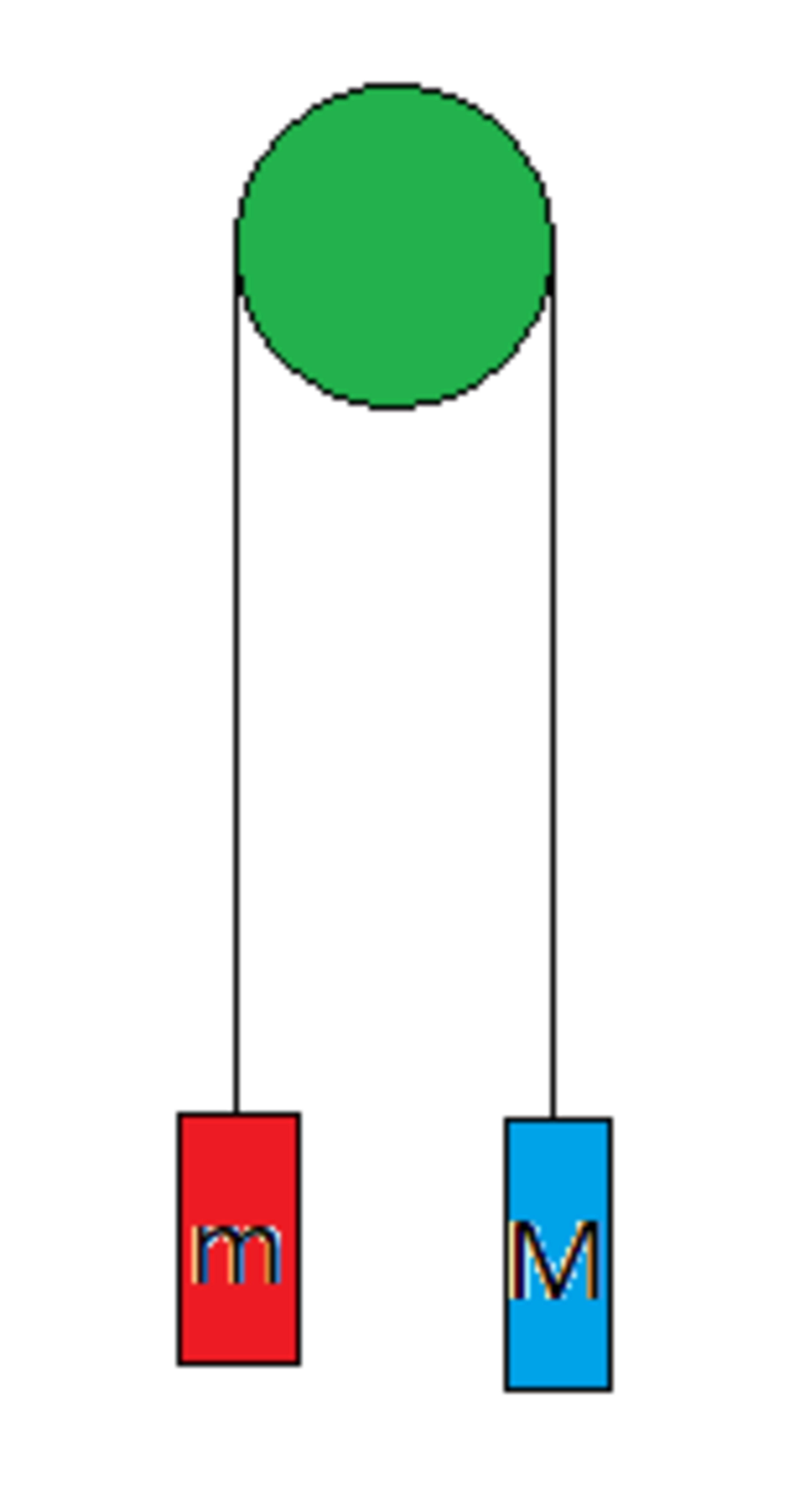 In the above pulley-mass system the mass
constantly decreases with a rate of
.
In the above pulley-mass system the mass
constantly decreases with a rate of
.
If initially both the masses were equal to , then find the distance travelled by the mass in meters in assuming that the mass didn't reached the top end in those and .
The answer is 0.225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the mass m decreases at constant rate α = 0 . 0 1 g s − 1 and at the beginning m ( 0 ) = M , we can write:
m ( t ) = M − α t
The force on the system is:
F = ( M − m ( t ) ) g = ( M + m ( t ) ) x ¨ ⇒ x ¨ = M + m ( t ) ( M − m ( t ) ) g
x ¨ = 2 M − α t α g t , with boundary conditions x ( 0 ) = 0 and x ˙ ( 0 ) = 0
It's easy to integrate that expression twice in order to get x ( t ) :
x ( t ) = 2 α 2 α t ( 4 M − α t ) + 4 M lo g ( 2 M ) ( α t − 2 M ) + 4 M ( 2 M − α t ) lo g ( 2 M − α t ) g
Using the values provided in the text, we fine x ( 3 0 s ) = 0 . 2 2 5 m .