Charge density!
A thin insulating rod with charge density λ=+5 nC/m is arranged inside a thin conducting cylindrical shell of radius R=3 cm. The rod and shell are on the same axis, and you can assume they are both infinite in length.
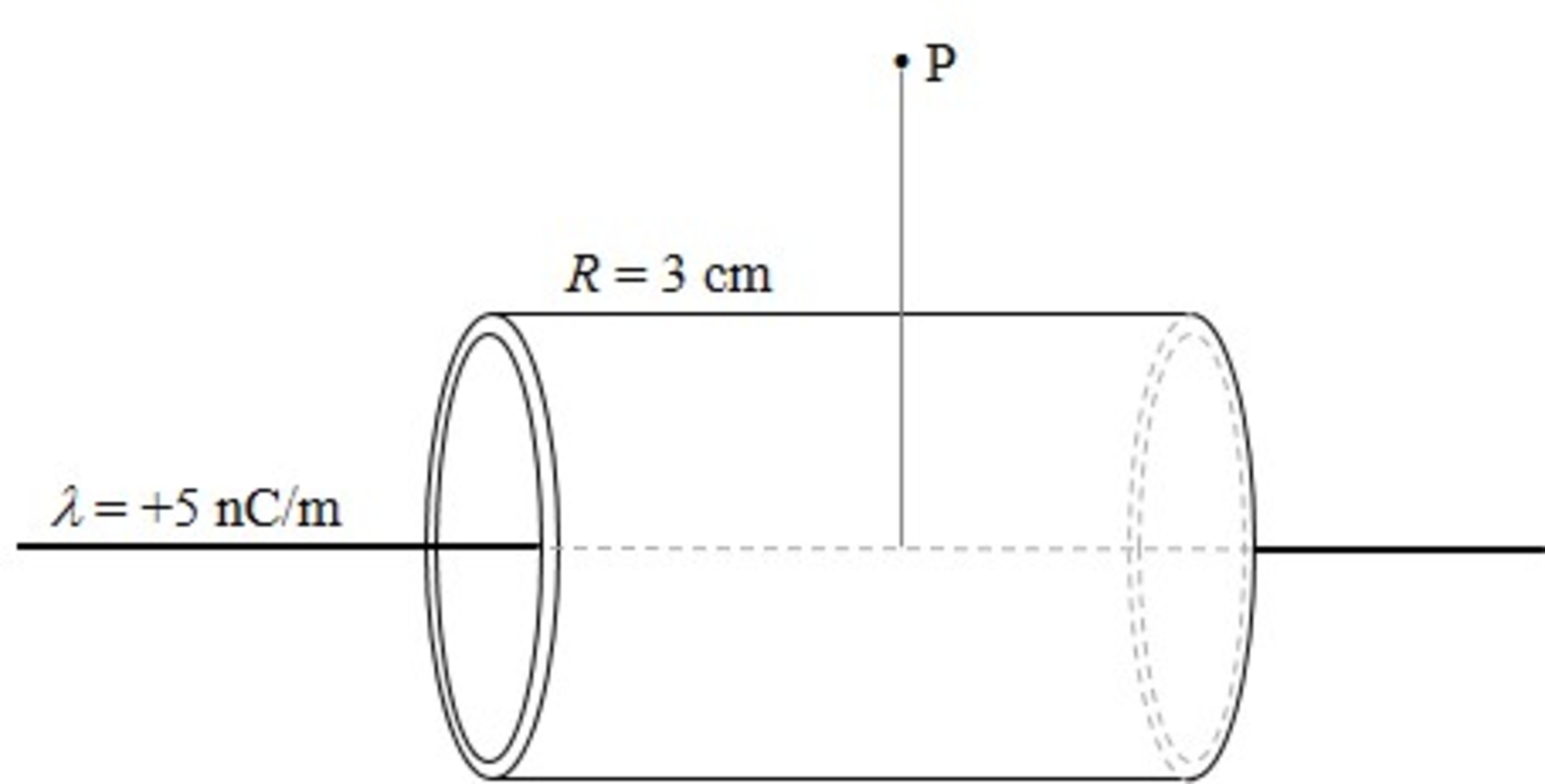
What is the SURFACE charge density σ induced on the OUTSIDE of the conducting shell in nC/ ?
The answer is 26.53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a very long section of the rod and shell, of length L > > R so that boundary effects are negligible.
Choose a Gaussian surface: S inside the the conducting shell. Since the field in a conductor is zero, the total flux through S is Φ = 0 , so the enclosed charge is also zero.
This is the sum of the negative surface charge − A σ on the inside of the shell and of the positive charge L λ of the rod: A σ + L λ = 0 . Since the net charge on the shell is supposedly zero, the positive surface charge on the outside is + A σ .
(In other words, the outside surface charge on the shell is equal to the charge of the rod inside .)
We obtain σ = A L λ = 2 π R L L λ = 2 π R λ = 2 π ⋅ 0 . 0 3 m 5 n C / m = 2 6 . 5 3 n C / m 2 .