Charge on Plates
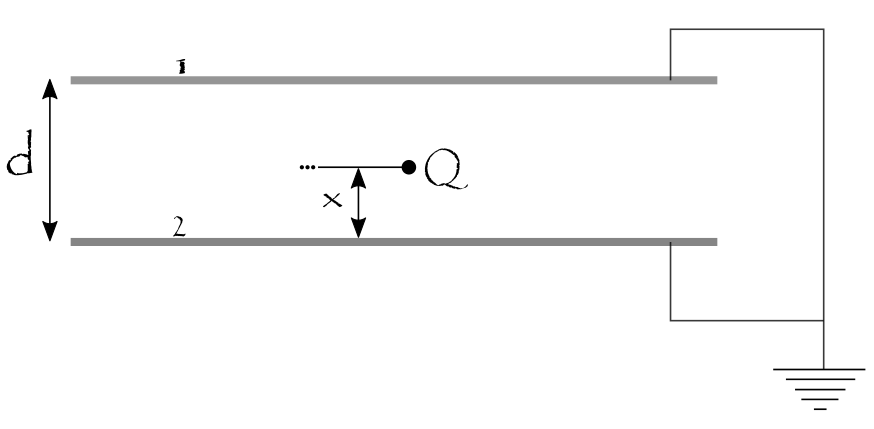
A parallel plate capacitor has plate area and distance between plates . Both the plates of a parallel plate capacitor are earthed and a charge is placed at a distance from lower plate (plate ).
Find the ratio of charge appearing on plate 2 to charge appearing on plate 1.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the charge Q is moved parallel to the plates, the charges induced on the other plates will remain the same. However its distribution will change. Lets spread the charge over the plate area.
The configuration so formed is same as two capacitors short circuited (as one plate is shared and others are at same potential (0)). Thus sum of charges on plate 1 and plate 2 mus be − Q .
Let the charge on bottom plate be q and top plate be − Q − q .
Since both capacitors are short circuited, potential drop across them must be same. x ϵ o A − q = d − x ϵ o A Q + q − q x = q d − q x + Q ( d − x ) q = d − Q ( d − x ) For x = 3 d , q = 3 − 2 Q and − Q − q = 3 − Q
the required ratio is 2 .