Charge Seesaw 2
A structure consists of three massless rigid rods of length , which have a fixed angular separation of degrees (see diagram). Three identical point-particles of mass and charge are attached at the ends of the rods. The center of the structure is hinged at the origin of the plane, such that it can rotate freely about the origin. There is another particle of charge fixed at position . The Coulomb constant is .
At time , the structure is at rest, and one of the rods is aligned with the axis. Find the time period of motion.
Details and Assumptions:
1)
2)
Neglect all forces except for the standard electric Coulomb force
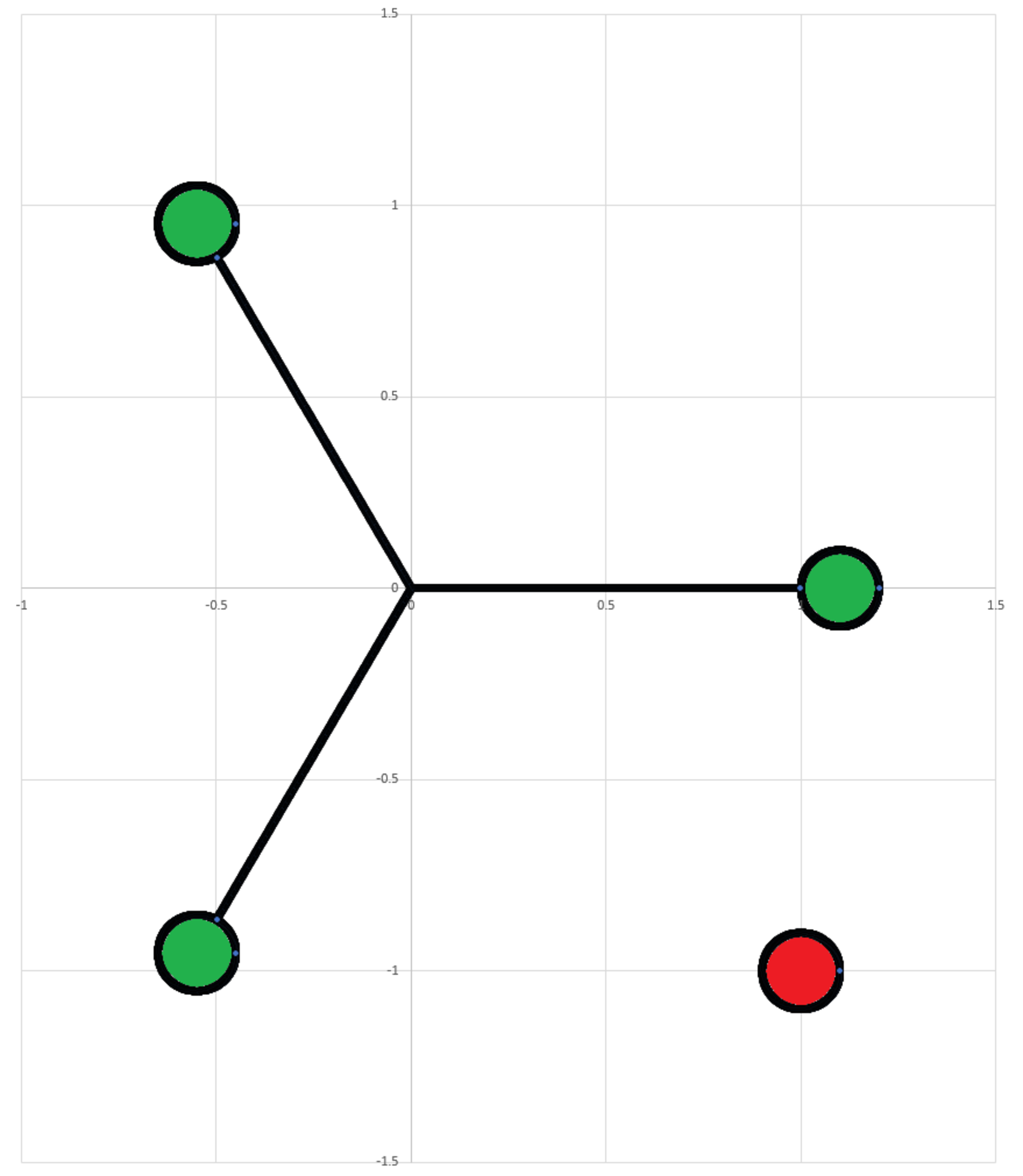
The answer is 7.094.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At any general time t , let the coordinates of the charges be:
r 1 = ( cos θ sin θ ) r 2 = ( cos ( θ + 3 2 π ) sin ( θ + 3 2 π ) ) r 3 = ( cos ( θ + 3 4 π ) sin ( θ + 3 4 π ) ) r 0 = ( 1 − 1 )
The velocities of each of the particles are:
v 1 = d t d r 1 ; v 2 = d t d r 2 ; v 3 = d t d r 3
The kinetic energy of the system is:
T = 2 m ( ∣ v 1 ∣ 2 + ∣ v 3 ∣ 2 + ∣ v 3 ∣ 2 ) = 2 3 θ ˙ 2
The total potential energy of the system is:
V = ∣ r 1 − r 0 ∣ k e q 2 + ∣ r 2 − r 1 ∣ k e q 2 + ∣ r 2 − r 0 ∣ k e q 2 + ∣ r 3 − r 1 ∣ k e q 2 + ∣ r 3 − r 2 ∣ k e q 2 + ∣ r 3 − r 0 ∣ k e q 2
At time t = 0 , the system is at rest at θ = 0 , so θ ˙ ( 0 ) = 0 . At this orientation, let the potential energy of the system be V i . To solve this problem, I once again exploit the fact that the system oscillates between equipotential points. In this case, the potential energy of the system at θ = 3 0 ∘ is the same as the initial potential energy. This can be visualized as the system is similar in terms of distances relative to the fixed charge, as all charges and masses are identical. Thus, it can be concluded that the system oscillates between θ = 0 and θ = 3 0 ∘ and the system moves from one extreme position to another in half the time period. Now, applying the law of conservation of energy gives:
T + V = T i + V i ⟹ T + V = V i ⟹ θ ˙ = 3 2 ( V i − V )
Separating variables and integrating gives:
∫ 0 π / 6 2 ( V i − V ) 3 d θ = ∫ 0 T / 2 d t
Solving the monster numerically:
T ≈ 7 . 0 9 3
One can also plot the potential energy as a function of θ to identify the equipotential points.
One can see that as θ > 3 0 ∘ , the potential energy exceeds it's initial value, which is physically impossible as there is no other external energy source mentioned in the problem statement. Between zero and thirty degrees, the PE is always lower than it's initial value as some of it is converted to kinetic energy as per the conservation of energy principle.