Charge Seesaw
Two identical particles of mass and charge are attached at opposite ends of a massless rigid rod of length . The center of the rod is hinged at the origin of the plane, such that the rod can rotate freely about the origin. There is another particle of charge fixed at position . The Coulomb constant is .
At time , the rod is at rest, and it is parallel to the axis. Find the time period of the rod's motion.
Details and Assumptions:
1)
2)
Neglect all forces except for the standard electric Coulomb force
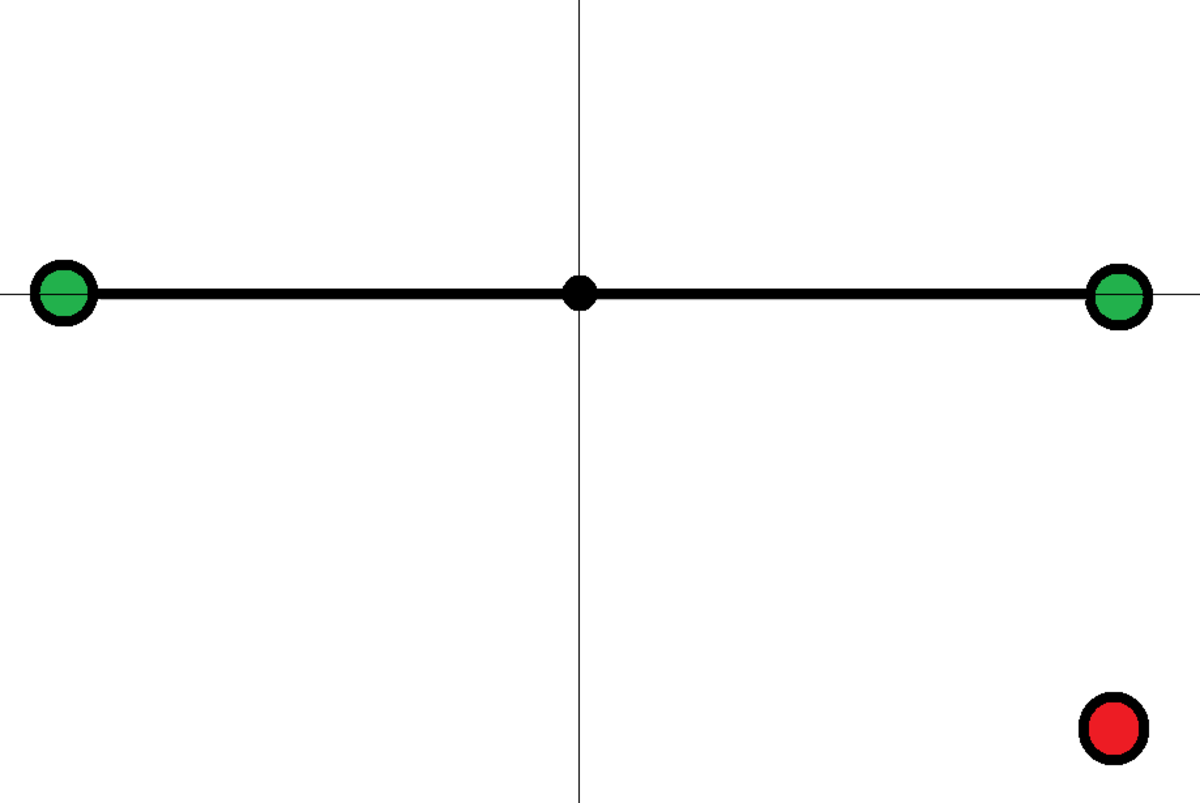
The answer is 8.689.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a moment at time t where the rod makes an angle of θ with the horizontal. At this configuration, the coordinates of each of the masses are:
r 1 = ( cos θ sin θ ) r 2 = ( − cos θ − sin θ )
Velocities are:
v 1 = θ ˙ ( − sin θ cos θ ) v 2 = θ ˙ ( sin θ − cos θ )
The total electrostatic potential energy of this system of three charges in this configuration is:
V = ( 1 − cos θ ) 2 + ( 1 + sin θ ) 2 1 + ( 1 + cos θ ) 2 + ( 1 − sin θ ) 2 1 + 2 1
The total kinetic energy of this system is:
T = 2 m ∣ v 1 ∣ 2 + 2 m ∣ v 2 ∣ 2 ⟹ T = θ ˙ 2
It can be seen that: θ ( 0 ) = θ ˙ ( 0 ) = 0 . Applying the conservation of energy equation leads to:
T + V = T i n i t i a l + V i n i t i a l
This gives:
θ ˙ 2 = 2 1 + 1 + 5 1 − V θ ˙ 2 = 2 3 + 5 1 − V
As time progresses, θ will increase since the charge on the right is initially closer to the fixed charge and will experience a greater upwards repulsive force that sets the system into motion.
⟹ θ ˙ = ( 2 3 + 5 1 − V ) 1 / 2
Now, with a little bit of visualization, one can imagine that as the rod rotates by 90 degrees, it's configuration will be similar to it's initial configuration in the sense that the potential energy of the system at that instant will be similar to the initial potential energy. If the rod were to rotate beyond 90 degrees, the potential energy must increase as the movable charge comes closer to the fixed charge. An increase of PE would violate the energy conservation equation, which is a physical impossibility. Thus, the rod rotates from zero to 90 degrees and back to complete one full oscillation. Moving from zero to 90 degrees will be done in half a time period. Therefore, this half time period can be computed by separating and integrating the above equation as follows:
∫ 0 π / 2 ( 2 3 + 5 1 − V ) 1 / 2 d θ = ∫ 0 T / 2 d t
The evaluation beyond this point is done numerically.
T ≈ 8 . 6 8 9 4 6 6 5 1 1 6 6 4 9 6 2