Charged beads
Two 1-g beads with charges Q x = 2 μ C and Q y = − 3 μ C slide on (without friction) two perpendicular wires ( x and y axes). The charges are initially located at ( 5 m , 0 ) and ( 0 , 3 m ) and released from rest.
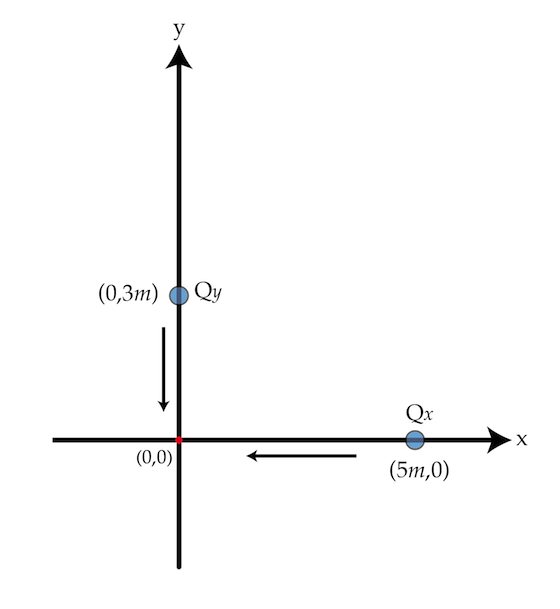
What is the distance in meters between the charges when Q y crosses the origin ( 0 , 0 ) ?
Details and assumptions
k = 4 π ϵ 0 1 = 9 × 1 0 9 N m 2 / C 2
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Yep, that's how I did it too. Good work.
What about the gravitational force acting on Qy ? And since the particles are constrained to move along the y axis and x axis, shouldn't we be looking at each axis separately , i.e Qy moving along y with r^2 becoming y^2. One issue is that we need to find the time at which y crosses the x axis and we are given the force (and hence the acceleration) as a function of r. Should we take the reciprocal (giving dt/dv and integrate it from v=0 to the max (possibly by using the idea that all potential energy is converted to kinetic)
How the answer changes if, we take gravitational force on Qy into consideration.
There is no external torque on the system so the angular momentum is conserved ( L ˙ = τ n e t = 0 ). The angular momentum is clearly zero in the initial condition and so, must be zero throughout.
Let's calculate the angular momentum about the center of mass. If 2 x is the coordinate of the particle Q x and 2 y is the coordinate of Q y , the center of mass is given by ( x , y ) .
At any given time, the net angular momentum is given by m v y x − m v x y = 0 (for the clockwise movement of Q x at the perpendicular distance y and the counter-clockwise movement of Q y at the perpendicular distance x ).
Equivalently, we have y ′ x − x ′ y = 0 which implies
d t d y x = 0 .
Therefore, y x is constant and the particles must cross the origin concomitantly.
Great solution bro!I liked the atypical style of solving instead of writing the standard differential equations.
We begin by writing Newton's Second Law for each bead. For the bead on the y-axis, we have ( d t 2 d 2 y ( t ) ) m = − K q 1 q 2 ( ( x ( t ) ) 2 + ( y ( t ) ) 2 ) − 1 . 5 y ( t ) where q1 and q2 are the absolute values of the charges. Note that we are only interested in the y-component of the force acting on the bead. This is where the extra x 2 + y 2 y factor comes from. In a similar manner, we calculate the x-component of the force acting on the other bead and arrive at: ( d t 2 d 2 x ( t ) ) m = − K q 1 q 2 ( ( x ( t ) ) 2 + ( y ( t ) ) 2 ) − 1 . 5 x ( t ) . We notice a certain symmetry in these equations: although the bead on the x-axis is farther away from the origin, it experiences the greater force. It seems plausible that this greater force balances out the bead's greater distance. Thus we would expect both beads to arrive at the origin simultaneously. Let us see if we can make this thinking rigorous. We begin by dividing eqt (1) by (2) to get d t 2 d 2 x ( t ) d t 2 d 2 y ( t ) = y ( t ) x ( t ) . Now comes the key step: We notice that equations (1) and (2) are identical except that the x's and y's are switched. Therefore we conclude that x(t) has the same functional form as y(t), differing only by a constant factor determined by the initial conditions. Remembering this fact, we can perform a series expansion of d t t d t x ( t ) d t t d t y ( t ) about t = 0. Due to symmetry conditions, all the terms in the expansion vanish except the lowest order. This leads to the following equation: a x ( 0 ) a y ( 0 ) = x ( t ) y ( t ) where ay(t) is the acceleration of the bead on the y-axis, and ax(t) is the acceleration of the bead on the x-axis. But the ratio of accelerations at t = 0 is simply 5/3, and so 5 / 3 = x ( t ) y ( t ) → x ( t ) = 3 / 5 y ( t ) for all t. And so when y(t) = 0, x(t) = 0, and the distance between the beads is 0.
Let the position of the charge Q y be r 2 = y y ^ and that of charge Q x be r 1 = x x ^ . Let r = x 2 + y 2 denote the distance between the charges. Then, the equation of motion for charges Q x and Q y are m d t 2 d 2 x = − r 3 k Q x Q y x , m d t 2 d 2 y = − r 3 k Q x Q y y .
Now consider the relative motion between the charges. Let r = r 2 − r 1 denote the relative position. Then, the above equations for each of the charges can be combined to one equation for relative motion, m d t 2 d 2 r = − r 3 k Q x Q y r . This equation is exactly the equation of motion for a point charge getting attacted to another point charge of opposite sign fixed at origin. The resultant relative motion is a stright line towards the origin. Thus, when y coordinate of the relative motion becomes zero, x coordinate also becomes zero.
Let's examine the motion of the center of mass G of the two charges. G is influenced by the force of x-axis and y-axis. Furthermore, G is the middle of the distance between two charges. By some basic geometry, it is clear that the total force exerted on G always directs towards the origin O .Initial velocity of G is zero, so ultimately G will approach origin 0, that means both the charges are in the origin O
Suppose when the position of Q x and Q y is (x,0) and (0,y) respectively.
The acceleration of two charges respectively are:
a x = r 3 k Q x Q y x , a y = r 3 k Q x Q y y where r 2 = x 2 + y 2 .
We realise that a y a x = y x or x ′ ′ y − x y ′ ′ = 0 .
We have: ( x ′ y − x y ′ ) ′ = x ′ ′ y + x ′ y ′ − x ′ y ′ − x y ′ ′ = 0 , so x ′ y − x y ′ = constant .
We know that intially x ′ = y ′ = 0 , so x ′ y − x y ′ = 0 .
We have: ( y x ) ′ = y 2 x ′ y − x y ′ = 0 , so y x = constant .
This means that 2 charges will reach (0,0) at the same time and the answer is 0.