Charged Ring Over An Infinite Grounded Plane
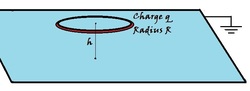 A thin ring of radius
is charged with a charge
. It is then placed over an infinitely large
grounded
conducting plane at a height
, as shown in the figure above.
A thin ring of radius
is charged with a charge
. It is then placed over an infinitely large
grounded
conducting plane at a height
, as shown in the figure above.
Find the magnitude of the surface charge density (in C/m ) of the induced charge at the point on the plane which is exactly below the ring's center.
Details and Assumptions
The answer is 0.000008149.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We could use the method of image to solve it. Since we are dealing with infinite plane, then by partitioning the circular wire into very small elements, we conclude that the image is also a circular wire with radius R and charge − q located at distance h below the plane.
The electric potential of a circular wire with charge q and radius R at the point located in a line passing through the center of the wire is given by V ( z ) = 4 π ϵ 0 q R 2 + z 2 1 where z is the distance between the point and the center of the wire.
Now, let take the origin at the center of the image circular wire and z-axis is the line that connecting the center of the wire and it's image. Using formula above, we could write the electric potential at the point located in z axis as, V ( z ) = 4 π ϵ 0 q ( R 2 + ( 2 h − z ) 2 1 − R 2 + z 2 1 )
And the induced surface charge, σ = − ϵ 0 ∂ z ∂ V ∣ ∣ ∣ ∣ z = h or σ = − 2 π ( R 2 + h 2 ) 3 / 2 q h and finally we have, ∣ σ ∣ = 8 . 1 × 1 0 − 6 .