Charges On a Ring
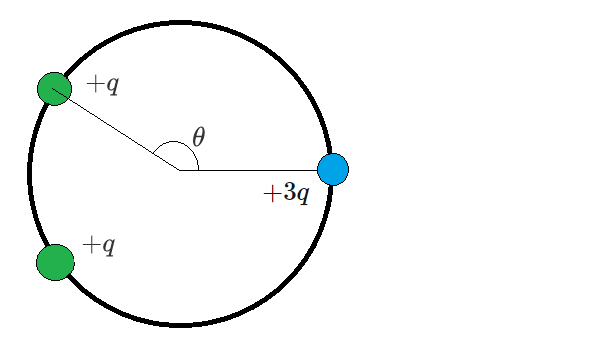
Three massless, charged point-particles (two with charge + q and one with charge + 3 q ) are situated on a friction-less circular ring.
The + q charges are both separated from the + 3 q charge by an angle of θ .
If all three charges are in stasis, what is the value of θ (in degrees, to 1 decimal place)?
Note: Feel free to use a computational aide as necessary.
The answer is 134.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
+1! .The charges are constrained to move only along the circumference of the ring, so solving for net force vector (due to charges) normal to ring would also do.
Log in to reply
Do you mean the net force on any particle must be in the direction of normal to the surface at that point ?
If so, how is it equivalent to minimum potential energy of the system !
Log in to reply
I mean net force d u e t o a l l c h a r g e s is normal to surface. if the resultant force due to charges is not normal to the tangent it will have some component along the tangent. Since no friction, this would cause the charge to move on circumference of ring suggesting that the potential energy not minimum. Since condition of equilibrium itself is net force zero. How is net force zero? if the resultant force due to the charges is normal to ring, the ring will apply equal and opposite force, nullifying the net force.
Whoa!!! i did by balancing force your solution is awesome bro It didnt came to my mind
A conventional solution by balancing forces: Denote the top +q charge to be vertex A, the bottom +q charge to be vertex B and the +3q charge to be vertex C. Let the centre be O. By symmetry, we have ∠ A O C = ∠ B O C = θ Now consider vertex A. The charge there will experience repulsive forces in the direction B A and C A . By simple geometry, ∠ B A O = θ − π / 2 , ∠ C A O = π / 2 − θ / 2 . Now, balancing forces in the tangential direction, we obtain ( 1 − cos ( 2 π − 2 θ ) ) ( sin ( θ − π / 2 ) ) = ( 1 − cos ( θ ) ) ( 3 sin ( π / 2 − θ / 2 ) ) Solving this, we get the answer.
We want to minimise the electrostatic potential energy of the system. Thus we want to minimise V = 8 π ε 0 r q 2 { sin θ 1 + sin 2 1 θ 6 } where r is the radius of the ring, and d θ d V = − 8 π ε 0 r q 2 × sin 2 θ cos θ + 1 2 cos 3 2 1 θ so we need to solve the equation 1 2 cos 3 2 1 θ + cos θ = 0 . The numeric solution to this equation is θ = 1 3 4 . 3 7 5 7 9 1 7 ∘ .