Charges set up in a tetrahedron

Let me define the side-length of the tetrahedron to be L. Also, I will be using a system of units where the constant in coloumb's law is equal to 1 (because the units cancel out in the expression we are trying to find).

Consider the net force on one of the vertex-charges in the $\hat J$ direction as shown in this picture ( $\hat J$ points in the plane of one of the faces of the tetrahedron).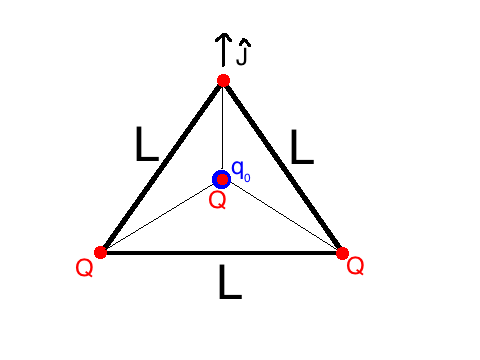

The net force from the other two vertex-charges in the same plane as $\hat J$ will be $2\frac{Q^2}{L^2}\sin(\pi/3)=\sqrt{3}\frac{Q^2}{L^2}$ and this net force is in the $\hat J$ direction.

The component of the force from the remaining vertex-charge in the $\hat J$ direction will be $\frac{Q^2}{L^2}\frac{x}{L}$ where x is the distance from the vertex to the center of an equilateral triangle. It can be shown that $x=\frac{L/2}{\cos(\pi/6)}=\frac{L}{\sqrt{3}}$ therefore the net force in the $\hat J$ direction on one vertex-charge from the other 3 vertex-charges is:

$\sqrt{3}\frac{Q^2}{L^2}+\frac{1}{\sqrt{3}}\frac{Q^2}{L^2}=\frac{4}{\sqrt{3}}\frac{Q^2}{L^2}$

Since the charges are in equilibrium, the net force from the central-charge $q_0$ in the $\hat J$ direction $\vec F_{q_0\rightarrow Q}\cdot \hat J$ must equal the (negative of the) above expression.

It is clear that $\vec F_{q_0\rightarrow Q}\cdot \hat J=\frac{-q_0Q}{\ell ^2}(\frac{x}{\ell})$ where $\ell$ equals the distance from a vertex to the center of the tetrahedron (and $x$ is the same as before).

To find $\ell$ I first found the height of the tetrahedron $y=\sqrt{L^2-x^2}=\sqrt{\frac{2}{3}}L$ . I then noted that $\ell^2=(y-\ell)^2+x^2$ therefore $\ell=\sqrt{\frac{8}{3}}L$ and so $\vec F_{q_0\rightarrow Q}\cdot \hat J=\frac{-16\sqrt{2}Qq_0}{9L^2}$

(Some of what I've said may not make sense until you think about it visually.)

Thus our equilibrium constraint is $\frac{-16\sqrt{2}Qq_0}{9L^2}=\frac{4Q^2}{\sqrt{3}L^2}\Rightarrow \frac{Q^2}{q_0^2}=\frac{32}{27}$