Charges wants freedom!

Consider this free body diagram for either sphere -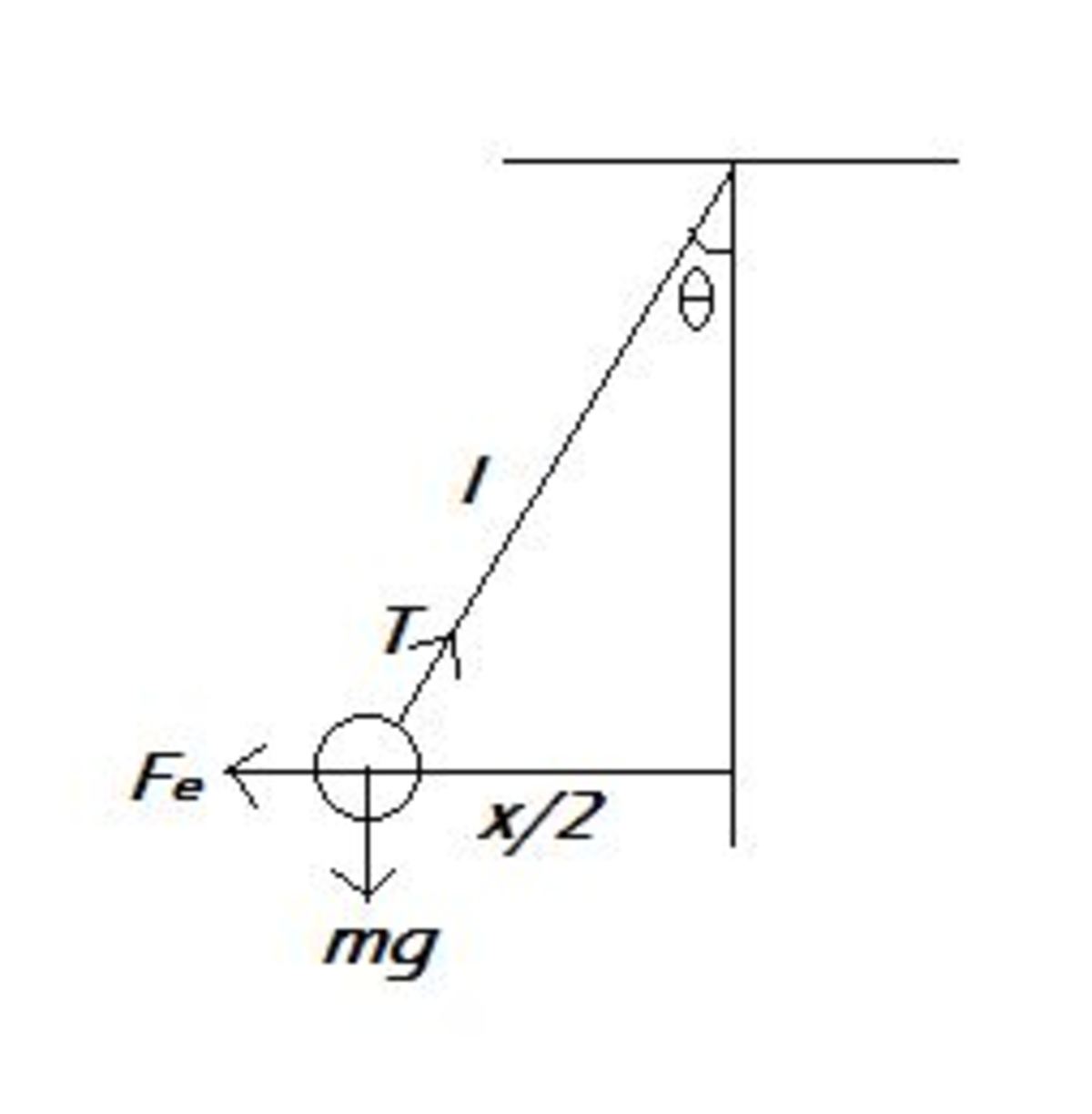

Considering the components perpendicular to tension (T) , $F_e \cos(\theta) = mg\sin(\theta) ...(i)$

(As the spheres are in equilibrium before charge starts leaking out)

Now, as 'x' is very small compared to 'l' , $\theta$ is very small. Thus, (i) can be rewritten as -

$F_e = \frac{mgx}{2l}$

$\Rightarrow \frac{q^2}{4\pi\epsilon_{0}x^2 } = \frac{mgx}{2l}$

$\Rightarrow q = \sqrt{\frac{2mg{\pi}{\epsilon_{0}}x^3}{l}}$

$\Rightarrow \frac{dq}{dt} = \frac{3}{2}\sqrt{\frac{2mg{\pi}{\epsilon_{0}}x}{l}} \frac{dx}{dt} ...(ii)$

Now,

$\frac{dx}{dt} = v = \frac{C}{\sqrt{x}}$ $\Rightarrow \sqrt{x}\frac{dx}{dt} = C$

Therefore, (ii) becomes

$\frac{dq}{dt} = \frac{3}{2}C\sqrt{\frac{2mg{\pi}{\epsilon_{0}}}{l}}$

By comparison, $a=3, b=2, f=2$ $\Rightarrow a + b + f = 3 + 2 + 2 = \color{#20A900}{\boxed{7}}$