Chat Six

Probability Level 5

Chat Six is an application that allows you to invite 6 friends to chat in your private chat room online. Your friend then can create his or her new chat room and invite any 6 friends (including you) into it. Therefore, it is possible for you and your online friend to have at most 5 mutual friends in 2 different chat rooms.

As the community grows larger, every member eventually has 1 chat room of their own (each consisting of 7 persons), and if we pick any 2 persons out of this network (friends or not), they will have 2 mutual friends in common.

If n n is a number of people in this entire social network, what is the least possible value of n n ?

Assume there is no deletion of any room or member along the way.


The answer is 16.

Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In order to minimize the value of n, for any 2 persons a and b, if a invite b into a's room, b will invite a into b's room, too. By doing so, we can symbolize all the people in the network as nodes or vertices, connected together with edges or connections, in the graph theory with n = number of vertices.

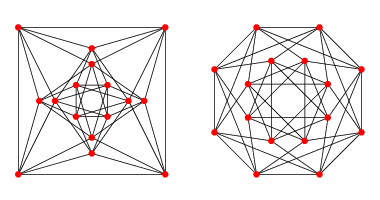
When we construct graph G: (V , E), where V stands for vertex and E for edge, each vertex will have 6 edges connecting to other 6 nodes. We then have a regular graph of valency or degree of 6 (6 edges), and with a constraint that any 2 vertices share the same amount of mutual nodes, it means that this graph is also a strongly regular graph or a graph that shares the same amount of adjacent elements.

With a strongly regular graph G(V , k , λ, μ) = G(V , 6 , 2 , 2), where k is the degree, λ = amount of mutual friends between 2 connected nodes(friends), & μ = amount of mutual friends between 2 non-adjacent nodes (non-friends), we can calculate V with a formula:

(V - k - 1)μ = k(k - λ - 1)

2(V - 6 - 1) = 6(6 - 2 - 1) = 18. Thus, V = 16.

The illustrative graph is as shown:

2 Helpful 0 Interesting 0 Brilliant 0 Confused

One solution for those who are unfamiliar with the graph theory (just like I am), can be the following. Using nodes to represent people and lines as connections (Just like the above solution). We can easily see that for two friends to have exactly two mutual (common) friends each line should be a common side of two triangles(Just like a tetrahedron). So if we can make some structures with the help of tetrahedron in which each node is exactly a part of two tetrahedron then all the conditions of the type of network asked in the question will be fulfilled.

If we connect the corners of the (Four squares attached to the four corners of a central square like chess board). Then the diagram we get satisfies all the conditions in the questions and we can see that the minimum number of people is 16. (Sorry for not being able to put the diagram because there is no option to put diagrams.)

dhiraj agarwalla - 5 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...