Cheating With A Valentine Cake
A mother brings home a surplus Valentine Cake from the bakery where she works.

It's made from 3 semi-circles of radii 2, 3, 5 inches, 3 inches thick. See graphic
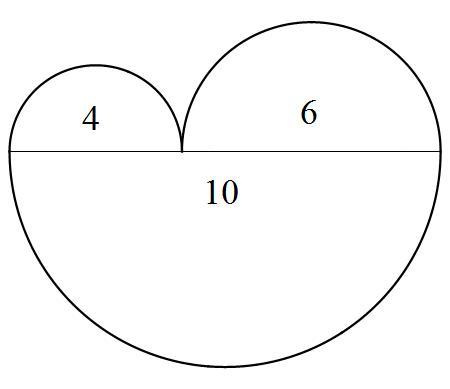
It has a rich red frosting on top and on the vertical sides. She decides to feed it to her two boys. But she knows that they are going to both want the same amount of cake and the same amount of frosting. She realizes that she cannot divide the cake in half with one straight vertical cut into just 2 pieces that both have the same cake volume and frosting surface area. So, picking a point on the perimeter of the cake, she makes 2 straight almost vertical cuts from it (the 2 cuts meet at the point she picks) dividing the cake into 3 pieces, and takes out the middle piece for herself, leaving 2 pieces for the boys that have exactly the same cake volume and frosting surface area. Let be the smallest cake volume of the piece she can cut out for herself. Cake is 3 inches thick.
Find .
Note : Any piece that contains the cusp of the cake can be considered to be a single piece, i.e., e.g. "two pieces" with the cusp point in common is one piece. Also, "vertical" refers to the axis of this solid.
Unhelpful Hint : You may want to look up the Ham Sandwich Theorem , of which the Pancake Theorem is the 2D version of it. According to these theorems, it should be possible for the mother to divide the cake in half with a single straight vertical cut, each half having the same volume and surface area, but here this doesn't apply. Why?
The answer is 972.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The 2 cuts are shown by the thin black lines. The angles indicate where the cuts start and end. The area of the center piece is 3 . 2 4 2 6 9 square inches, the volume being 9 . 7 2 8 0 7 cubic inches. From this, we have the answer 9 7 2 .
For both boys to have the same frosting area, their pieces must have the same frosted perimeters. Hence, notice that
2 ( 1 1 4 . 1 3 7 ) + 5 ( 1 1 3 . 2 6 8 ) = 5 ( 6 6 . 7 3 2 ) + 3 ( 1 5 3 . 6 5 1 )
For this arrangement of cuts, special attention must be given to ensure that the cusp does not fall outside the middle piece, or else there's 4 pieces, not 3 .
If one is permitted to cut the cake into 3 pieces with a single straight cut, then one boy can have one piece and the other boy can have the other two, and both will have exactly the same cake volume and frosting area. But that's 3 pieces, not 2 . That's why the Ham Sandwich Theorem doesn't apply here.