Check the Topic!

Imagine the figure to be 2-Dimensional with the cone to be a triangle and the cylinder to be a rectangle.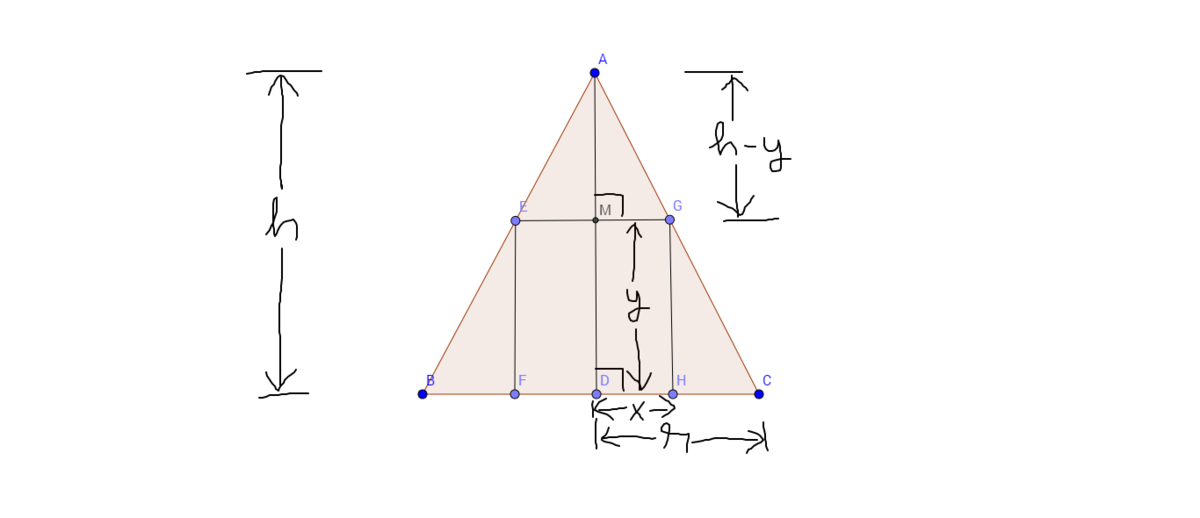 Since $\triangle ADC,\triangle AMG$ and $\triangle GHC$ are similar to each other,using similarity properties we get
$\dfrac{h}{r}=\dfrac{h-y}{x}=\dfrac{y}{r-x}$
From the first and the last term we get $y=\dfrac{h(r-x)}{r}$
Since the lateral surface area of a cylinder is $2\pi xy=\dfrac{2\pi xh(r-x)}{r}.$
Since the $\dfrac{2\pi h}{r}$ is constant,we bring it out. $L.S.A=\dfrac{2\pi h}{r}(rx-x^2)$
So we have to only differentiate $(rx-x^2)$ and equate it to $0$ so as to maximize the $L.S.A.$
After differentiating,we get $r-2x=0\Rightarrow x=\dfrac{r}{2}$ and plugging this in the equation we found earlier,we get $y=\dfrac{h}{2}.$
Therefore,the lateral surface area of the cylinder $=2\pi xy=4\pi=\boxed {12.57}.$