Checkerboard Area
The diagram below shows two identical, large squares divided into smaller squares.
Which area is larger, blue or green?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
47 solutions
The introduction states that the squares are identical , therefore areas are equal. Solution implies that the squares are similar!
Log in to reply
I didn't really imply the larger squares were only similar, bear in mind that congruence is a special kind of similarity. The smaller squares within the larger squares are similar though.
I agree, it says squares are identical. Surely then the areas have got to be identical?
Do you think we can do it without any calculations?
Log in to reply
Yes...
Clue : Consider the pattern for the right-hand square. Since the pattern is alternating, there is no way to achieve the same amount of area. If this is possible, then the shape must be the rectangle for both shapes to have same areas. Otherwise, the cuts are uneven in the square.
So if you superimpose the 3-by-3 square with the 5-by-5 square, the problem should be a piece of cake.
Log in to reply
You don't need to make the division of 5/9 or 13/25.
Always a fraction divided by a smaller number will be bigger than a same fraction divided by a larger one.
In our case, this applies since 1/9 > 1/25.
You just need to count and compare. Just like 1/10 will be always larger than 1/11
I did this too! Except I didn't convert the fractions to decimals to compare them. I compared them to 1/2. 13/25 is 1/50 (1/25/2) bigger than one half, whereas 5/9 is 1/18 (1/9/2) bigger than one half. 1/18 is bigger than 1/50, so 5/9 is bigger
I like this solution!
Poorly designed question....04 difference...really!
Log in to reply
The difference may be relatively small, but one area is larger none the less because of that difference. The only time where that difference is negligible is if we needed to round, which we obviously didn't.
The area of white and color is equal except the last color square, the odd one. The blue is bigger than the green, ergo.
Moderator note:
The comments had some concern about if the argument is valid. Here's an algebraic approach to the same idea. For simplicity and without loss of generality, we'll consider the overall area of each figure to be 1.
If we consider a colored square in one of the patterns to have an area of x , then the area of all the colored squares (excluding the last odd one out) is 2 1 − x . Putting the excluded square back in, the area is 2 1 − x + x . Note how the size is determined entirely by the size of x (the count of squares is irrelevant) and a larger x will indicate a larger colored area. Therefore the blue area is larger.
@Sridev Humphreys Cut the centre square in half and colour half of it white. Now the coloured and white areas are completely equal. So if you colour that half back in the colour it was originally, it's clear that the total coloured area is half the area of the full square, plus half the area of the central coloured square. Since the blue/white and green/white squares are the same size, these cancel out and you only have to compare the areas of the central squares. Though you are right that this does require maths; 1/3 > 1/5.
Hey that's really nice! I just posted my own solution, then read yours and upvoted it!
@Trejkaz your extra step in cutting the last square in half (and it could be any colored square, the middle or the last) does indeed plug the small hole in @Jeannine Myer 's solution. And it works because the two colored areas with the two half colored blocks are equal to one another and also equal to half the area of the large square. From there it is obvious and sufficient to recognize that that blue half square is larger than the green half square and the difference in the total blue and green areas is equal to the difference between the area of the two half squares which I also stated in my original comment (although I prefer your thought experiment over my formula).
My initial reasoning was pretty much identical to yours. (Or alternately put, green is "beating white" by just a little bit, whereas blue is "beating white" by a lot.) But after thinking about it a little more I switched to an explanation that I think is more proof-like and less reliant on common sense: in each case, the total area of the colored squares is one-half of the total plus one-half of one square.
I up voted your solution even though I suspected it was wrong ( or at least incomplete) because it was an interesting way of looking at the problem. The problem with your proposed solution is that the two colored areas excluding the last colored square in each figure are not equal. In fact the 12 green squares are larger in total area than the 4 blue squares (12/25 > 4/9). Your observation that the remaining blue square is larger than the remaining green square is true but you have to show that is large enough to make up for the fact that the squares counted so far yield a larger total area for green. In fact it does, but it requires math to do so (5/9 > 13/25). Interestingly for any two squares divided into n^2 and m^2 smaller squares (where, n not = m, n and m are >= 3, and both are odd) and colored in this way, the difference in the total colored areas between the two different larger squares is equal to 1/2 the difference in area between two of the different smaller squares. This can be easily proven using the equation for the ratio of the area of the small colored squares to total area of all smaller squares, which can be written as: ((n^2+1)/2)/n^2 = 1/2 + 1/2n^2.
What percentage does blue and green occupy?
- blue occupies 5 of possible 9 squares: 55.5%
- green occupies 13 of possible 25 squares: 52%
Blue wins!
If both large squares have the same area then to build one perfect blue square you will need exactly 4 green ones. If blue area is equal to the green area then green area must have at least 20 green squares. Since we have less then 20 green squares then blue area must be larger then a green one.
The bus driver's name was George!
Generalizing to any ( 2 k + 1 ) × ( 2 k + 1 ) checkering with center colored, all the colored areas are larger than 1 / 2 . The limit for k → ∞ monotonically goes to 1 / 2 . Hence, the coarser the checkering the larger the colored area.
I was wondering if anyone was going to use limits! To make it more precise, if p is an odd number, the ratio of colored squares to total squares is 2 p 2 p 2 + 1 . It is then easy to verify the limit that you mention.
I think the key point here is monotonicity, not the limit
suppose area of large square = 225
so area of blue square = 225 * 5/9 = 125
and area of green square = 225 * 13/25 = 117
Note. 15 * 15 = 225 , 5 is total blue squares, 9 is total squares in LHS square
13 is total green squares, 25 is total squares in RHS square
Method I used
Similarly, I just used 15 as the common factor for side length and came up with these whole units.
At school when we were comparing fractions e.g. 5/9 and 13/25 we were instructed to convert them to equivalent/common denominators. Therefore multiply denominators 9 * 25 = 225 to get the common denominator and we then multiplied the numerators to be equivalent 225ths which are 5 * 25 and 9 * 13 which gives Blue = 125/225 and Green = 117/225 hence blue is the larger area. Good old Mr Senior our maths teacher. :)
as the two squares are identical,their area is same.
so,the blue part has covered 9 5 portion of the square
and the green part has covered 2 5 1 3 portion of the square
9 5 = 0 . 5 6 and 2 5 1 3 = 0 . 5 2 , so, 0 . 5 6 > 0 . 5 2
so, the blue area is larger.
Typo: "there" -> "their"
So grateful for so many diverse and well-taught solutions ! :D
For a visual solution, first collapse all colored squares to one side:

Then draw a line down the center:

Finally, move as many half pieces from the less filled in side to "empty" spots on the more filled in side. Compare the remaining pieces on the unfilled side.

Ah, nice proof without words solution! I wasn't expecting this +1
In both cases, there is one more colored box than white boxes.
The number of colored boxes is 2 1 more than half of the total.
The total colored area is therefore half a box greater than half of the total area.
Since the green boxes are smaller than the blue boxes, the green area is less than the blue area.
The ratio of green:white is 13:12. The ratio of blue : white is 5:4 = 15:12 By looking at the ratios you can see that blue>green, 15>13. A no brainier.
Both of the fractions are 0.5 larger than the half of the denominator. Done.
What does this 0.5 signify?
Log in to reply
Half (0.5) of one ninth (1/9) vs half (0.5) of 1/25; i.e., half of a ninth is 1/18 and half of 1/25 is 1/50, but 1/18 is greater than 1/50 so blue is larger area.
We can assume the two big squares to have side 15 , each of the blue squares would have side 15/3 = 5, hence an area of 25.Whereas each of the green squares would have side 15/5 =3 and area 9.The total blue area would be 25 X 5 , which is greater than the green area, 9 X 13
Yep, choosing the side length to be 15 made the argument simple. To justify that this is a valid method, notice that one can always choose a suitable unit in which the length is 15 units.
You don't even need to make the division of 5/9 or 13/25.
Always a fraction divided by a smaller number will be bigger than a same fraction divided by a larger one.
In our case, this applies since 1/9 > 1/25. This since we counted and know that the difference between the squares is 5/9 - 4/9 = 1/9 and 13/25 - 12/25 = 1/25.
Just like 1/10 will be larger than 1/11 every time.
Blue = 5/9 of the total area. Green = 13/25 of the total area. Make the denominator the same to compare fractions, by multiplying 9 and 25. And change the numerator accordingly... Blue, 9 5 = 2 2 5 1 2 5 . Green, 2 5 1 3 = 2 2 5 1 1 7 . Therefore the blue is larger.
The colored squares are covering half a square more that half the chess-board. Since the blue squares are larger than the green ones that half extra blue square gives more area than the half green square.
Using basic observations, four squares from green make one square of blue and same goes to the white squares in green making one white square in blue. There are 4 white squares in blue requiring 16 small squares but green contains only 12 white squares and 5 blue squares requiring 20 small squares of green which only has 13, therefore the area of blue is larger.
Blue-White, 15-12 Green-White, 13-12
If you think about this as a pattern, with infinitely many squares each with more and more tiles than the last and all of them have the tile pattern, you know that as the sequence continues, the area of the colored section approaches 1/2. Knowing this, we can figure out that the green area is closer to 1/2 than the blue. All we have to do is figure out if the area of the blue is more or less than 1/2. And a quick count shows that the area of the blue is 5/9. And because 5/9 is greater than 1/2 and we know that the area of the green square is somewhere between 5/9 and 1/2 we know that the area of the green must also be less than 5/9.
Blue occupies 5/9, green occupies 13/25, multiply numerators by the denominators of the other fraction (to the get numerator when the denominators are the same): 5x25 = 125 for blue, 13x9=117 for green, blue has larger are (common denominator is 225)..
If you take the surface of a green square as a unit then the blue squares occupy 20 units and the green 13 units, the surface of the blue squares is bigger
Blue 5/9 = 125/225
Green 13/25 = 117/225
125 > 117
Blue is 5/9 ,& green is 13/25 on a denominator of 225 , blue is 125 and green is117
Imagine you could shift the colored squares to one side. Do so mentally.
Count the blocks in each of the box's left columns. 2/3 blue, 3/5 green. Or, 10/15 blue and 9/15 green.
I mentally slid the green ones onto each other and noticed there are not enough to reproduce all blue squares. Not the most analytical approach but it worked for this simple example...
Another approach would be to count the green squares and devide the number by four, since one green square equals 1/4 of a blue one. If the resulting number is smaller than five, they can't cover all the blue squares.
here's my take. Both squares are 50/50 color/white after the splitting of smaller and smaller squares approaching infinity. Green is just a few iterations closer to infinity so it's closer to being 50/50. Since blue is "less 50/50", and visually blue has more than white, it must have more area than green does.
Blue = 5/9 = 55% Green = 13/25 = 52%
If a big square area is 1 :
Green area is 13/25
-> wich is half + 0.5/25
Blue area is 5/9
->wich is half + 0.5/9
Since 0.5/9 > 0.5/25 Blue area is bigger !
Blue = 5/9 of the area; green = 13/25 of the area
The squares having equal areas, for example 1.
The area of the blue shaded area from the first square is 5/9 (=0.5 recurring, so 0.555555…).
The area of the green shaded area from the second square is 13/25 (=0.52)
So, the area of blue is larger.
Let's count white squares instead of color: left is 4/9, right is 12/25. 4/9 is equal to 12/27, which is easily comparable with 12/25 and 12/25 is greater. Therefore, white takes more area in the right square and subsequently less is left for the green, and as such, the blue color fills more area than green.
the blue squares represent 5/9th of total area: the green 13/25th. 5/9th is bigger than 13/25th
To find answer without a calculator:
Left square blue to white ratio 5/9 = 4.5/9 + 0.5/9 = 0.5 + 0.5/9 Right square green to white ratio 13/25 = 12.5/25 + 0.5/25 = 0.5 + 0.5/25 Subtract 0.5 from each equation we get left square = 0.5/9 vs right square = 0.5/25 Clearly 0.5/9 (left square) is larger since we're dividing the same number 0.5 by a smaller number ie 9.
It's easier than all of that. The blue square in the left diagram equals 4 unit squares in the right diagram. 5 blue squares times 4 units is 5x4=20 units In the green diagram there are 3 rows of 3 green squares and 2 rows of 2 green squares and so the area is (3x3)+(2×2) = 9+4=13 units 20>13 hence the blue area is greater
Areas equal, given. In blue square, blue larger by 5/9 - 4/9 =1 /9 In green square, green larger by 13/25 - 12/25= 1/25 1/9 is larger than 1/25, Therefore blue has most area.
Why are we subtracting the fractions? Shouldn't we be comparing 5/9 and 13/25?
OK. Look at it from a "mental picture" standpoint. Move all the colored tiles together at the top of each square. You can see that the area of the blue tiles covers 5 tile units on the square. If you do the same with the green tiles and overlay them mentally on the blue tiles, you would be 3 green tiles short to cover all the blue tiles. See! No calculations or calculator!
But the tiles are not of the same size. Isn't this going to be a problem?
It will monotonously converge toward 1/2 with increasing lines/rows and the blue is greater than 1/2.
Yep, but how does that tell us it is larger than the green area?
Nice work. I think it would be helpful and easier to follow if you added what the fractions mean
Looking at the white areas made this problem much easier using mental math...
Left white areas: 4/9, Right white areas = 12/25
Left white areas: 12/27, Right white areas = 12/25
With common numerators, Left has a smaller fraction of white areas, so blue has a larger area than green.
Correct answer is: The blue area is larger.
It is interesting to notice that the result is independent of the choice of a
If you assume each green square is one unit x one unit, then the area of a green square is one square unit. There are 13 green squares, so that is 13 square units. The blue squares are then two units on each side, so the area of each blue square is 2x2, or four square units. There are 5 blue squares, so five squares x four square units equals 20 square units. Blue area is larger, 20 square units vs.13 square units.
So, are you saying that four green squares comprise one blue square? I do not agree, can you explain why this is true?
Divide each large square into 15x15 smaller squares, then calculate how much of these smaller squares are covered by the blue and green areas. For the blue, each blue square is 5x5 = 25, so it's 25x5 = 125 small squares in total. For the green, each green square is 3x3=9, so it's 9x13 = 117 small squares. Hence blue covers greater area.
Yep, that is indeed a good way to visualize it
125:117 blue-to-green ratio
How did you get these numbers?
Green: 13/25, Blue: 5/9=15/27. Notice that 15/27=(13+1+1)/(25+1+1). Increasing both the numerator and denominator by 1 grows the numerator faster than the denominator. Thus, the numerator of Green +2 is larger than the denominator of Green +2, and the Blue fraction is greater.
Increasing both the numerator and denominator by 1 grows the numerator faster than the denominator.
Could you please explain what that means?
I think it would be helpful if you wrote down how you got these result
Let 15 (LCM of 3,5) be the side of larger square.
Blue area = (15/3) x (15/3) x 5 = 125
Green area = (15/5) x (15/5) x 13 = 117
Thus, Blue wins.
Yes, you can arrive at the answ e r b y calculating relative percentages also.
PS: If x is taken as the side of bigger square:
Area of blue squares = 9 5 × x 2 ≈ 0 . 5 5 6 × x 2
Area of green squares = 2 5 1 3 × x 2 ≈ 0 . 5 2 × x 2
Thus, Blue wins again! :P
Can you explain why we are calculating 15/(3 x 5 x 5)? What is this number?
Log in to reply
Definitely!
Please note that it's not 15/(3 x 5 x 5) but (15/3) x 5 x 5 = 125.
You could choose any length of the side of the bigger/outer square - side of length 1 or even a variable x. I have taken the LCM of 3 and 5 in order to get an integer when obtaining the sides of inner squares that would make calculations simpler. If the outer square has a side of length 15, we can calculate the side of the inner squares as follows:
Consider the upper side of the bigger square. There are 3 inner squares with their sides common with the square side. Thus, the side of each inner square is simply 15/3 = 5. If you'd have chosen x as the side of the bigger square, the answer would be x/3. The area of one square is 5 x 5 = 25. Since there are 5 such inner squares, the total area of the blue squares = 25 x 5 = 125. Similarly for the green ones = 3 x 3 x 13 = 117 where green squares have sides of length 15/5 = 3.
If you would have taken x as the length of side of bigger square, then:
Area of blue squares = 9 5 × x 2 ≈ 0 . 5 5 6 × x 2
Area of green squares = 2 5 1 3 × x 2 ≈ 0 . 5 2 × x 2
Thus, the LCM was taken to make calculations related to division simpler. Hope I was clear with the explanation. The method may seem more complex with this much explanation than simply calculating the percentages but once you've taken the LCM, the further estimations are much simpler.
Regards, Paras Lehana
Suppose both squares have unit area. By counting the squares it is easy to see that the areas are
blue = 9 5 green = 2 5 1 3
Now let's use our brains, not our calculators!
5 × 2 5 = 1 2 5 9 × 1 3 = 1 1 7
and so
5 × 2 5 > 9 × 1 3 ⟹ 9 5 > 2 5 1 3
and so the blue area is larger.
Another way to see the answer is to recognize the coloured areas as chunky overestimates to 2 1 . As the subdivision becomes finer the approximations approach 2 1 from above.
Why do we calculate 5 × 2 5 and 9 × 1 3 ? What do these quantities signify?
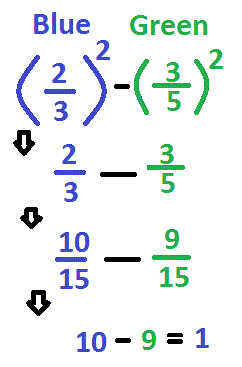
If both of the large squares have an equal area of 1, then we can simply find the areas of the blue and green areas by figuring out the how much of each square is shaded in.
Since 5/9 of the smaller squares in the first square are shaded in, the area would be 5/9, which is roughly 0.56
Since 13/25 of the smaller squares in the second square are shaded in, the area would be 13/25, which is roughly 0.52
In the end, the blue area is larger than the green area.