Checkerboard Tiling Game

Bob wins by ensuring that after his turn, there is always an even number of uncovered cells left. He can do this just with his $1 \times 1$ and $2 \times 2$ tiles.

Bob can easily force Ann to run out of spaces to play a $4 \times 4$ tile before he runs out of spaces to play a $2 \times 2$ tile**.

Once Ann can't use any more $4 \times 4$ tiles, she has to play a tile that covers an odd number of cells ( $1 \times 1$ or $3 \times 3$ ). This means Bob will ultimately win by playing a final $1 \times 1$ tile.

---

** There's a fair amount of case analysis here. Up to rotations/reflections, Ann has (if I've counted correctly) $22$ possible first moves. Of these, $19$ lose immediately (Bob can leave an even number of uncovered cells with no room for a $4 \times 4$ tile after his first go).

In the other three cases, Ann's first tile covers exactly one of the four central cells. Bob can't stop Ann playing a $4 \times 4$ tile after his first go, but he can after his second, and leave an even number of uncovered cells.

---

If Bob goes first, and they use the same tiles, he still wins: he just has to cover the four central cells with a $2\times 2$ tile on his first go.

If all the square tiles available had an odd number of squares ( $1 \times 1$ , $3 \times 3$ , and $5 \times 5$ ), then after each of Ann’s turns an odd number of squares of the checkerboard will be covered and after each of Bob’s turns an even number of squares of the checkerboard will be covered, and since the checkerboard has a total of an even number of squares, and since Bob can always place a $1 \times 1$ tile, Bob would win.

However, the presence of the $2 \times 2$ and $4 \times 4$ even tiles complicate things a bit, but Bob can still win if there are an even number of even tiles placed on the board by the end of the game. Since the only even tile Ann has is a large $4 \times 4$ tile, one of the strategies Bob can use is to block off all possible $4 \times 4$ positions and then evening out the number of even tiles played by placing his $2 \times 2$ even tile, if necessary. Here are four cases to consider depending on how Ann starts the game in relation to these four center tiles:

Case 1: On Ann’s first turn, she does not cover any of the four center squares.

That means Ann did not play a $4 \times 4$ tile, and Bob can place his $5 \times 5$ tile in one of the available corners. After this, Ann cannot play any $4 \times 4$ even tiles but only her $1 \times 1$ and $3 \times 3$ odd tiles. Bob can then win by playing only $1 \times 1$ tiles for the rest of the game.

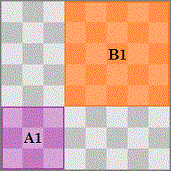
Case 2: On Ann’s first turn, she covers only one of the four center squares.

On his next turn, Bob should place his $2 \times 2$ tile to cover two of the other four center squares to block all but one of $4 \times 4$ positions left. If Ann places her $4 \times 4$ tile in the last available spot, and if there are an odd number of even tiles on the board, then Bob should play his $2 \times 2$ tile one more time, otherwise Bob should play his $1 \times 1$ tiles for the rest of the game. If Ann didn’t place her $4 \times 4$ tile in the last available spot, Bob should block it on his next turn, and then on his next turn if there are an odd number of even tiles on the board, he should play his $2 \times 2$ tile one more time, otherwise he should play his $1 \times 1$ tiles for the rest of the game.

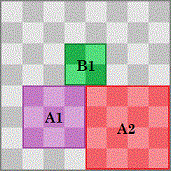
Case 3: On Ann’s first turn, she covers two of the four center squares.

On his next turn, Bob should place his $2 \times 2$ tile to cover the last two of the four center squares to block all the remaining $4 \times 4$ positions left. Then if there are an odd number of even tiles on the board, Bob should play his $2 \times 2$ tile one more time, otherwise Bob should play $1 \times 1$ tiles for the rest of the game.

Case 4: On Ann’s first turn, she covers all four of the four center squares.

Then there are no possible $4 \times 4$ positions left, but several $2 \times 2$ positions left. If Ann played her $4 \times 4$ tile on her first turn, then Bob should play his $2 \times 2$ tile on his next turn and $1 \times 1$ odd tiles for the rest of the game. If Ann did not play her $4 \times 4$ tile on her first turn, then Bob should play his $1 \times 1$ tiles for the rest of the game.

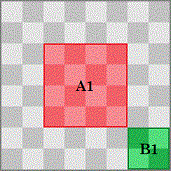
In all cases, Bob will win the game.

What if the board were 9-by-9?