Cheesecake Riddle
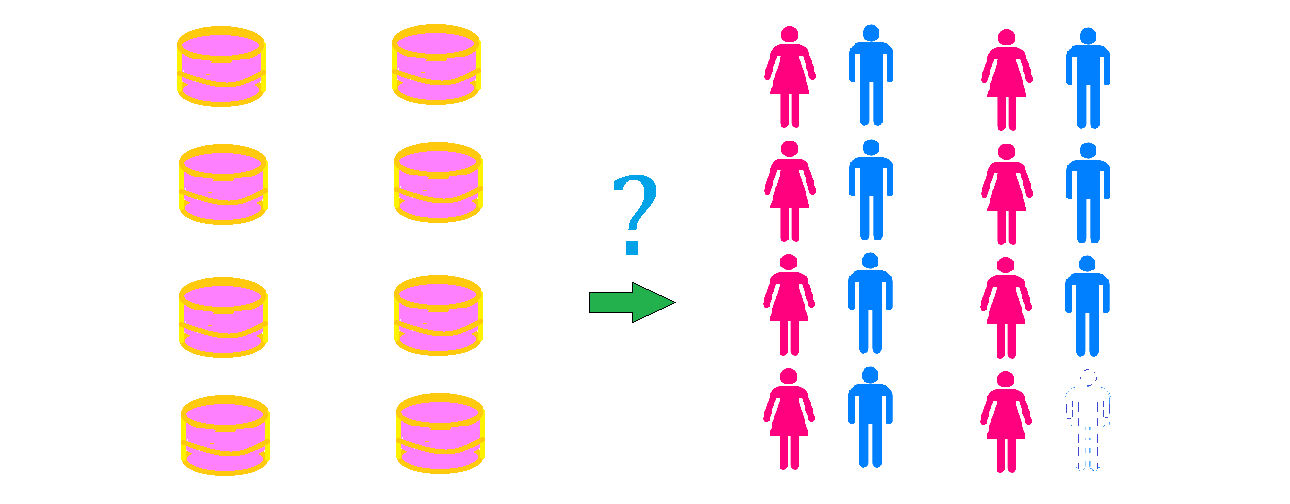
You invited of your friends to your party. You've already baked congruent strawberry cheesecakes so that each cake could be split into equal pieces and everyone would then get an equal share of cake.
However, one of your friends did not show up. Still, you intended to divide each cake into smaller equal pieces (not necessarily the same size for every cake) such that everyone could still get an equal amount of cake, but you didn't want to cut any cake into more than pieces, for it would ruin the cake texture.
What would be the minimum number of pieces you needed to cut?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Egyptian Fractions
To divide 8 cakes for 1 5 people, each person would acquire 1 5 8 amount of cake.
Now if we split the cakes into halves as previously intended, we will have one half left (the absent guest's one). Intuitively, that half may be divided further into 1 5 pieces for equal contribution, but we have only limitation of 1 2 cuts. So this is not allowed. Arithmetically, this concept could be expressed as: 1 5 8 = 2 1 + 3 0 1 .
It is clear that we have to limit the denominators to be under 1 2 , and with 1 5 as a common multiple, there are only two factors: 3 & 5 .
Obviously, 1 5 8 = 3 1 + 5 1 , and these are the least possible denominators combination, which will result in the least number of cuts in this case.
Thus, practically, we will first take 3 cakes and divide into 5 smaller cuts each, with total of 1 5 pieces. Then we will the remaining 5 cakes and divide into 3 pieces each, also with total of 1 5 pieces, as shown below:
Finally, each guest will take the one-third piece and the one-fifth piece, and everyone will get an equal share as desired.