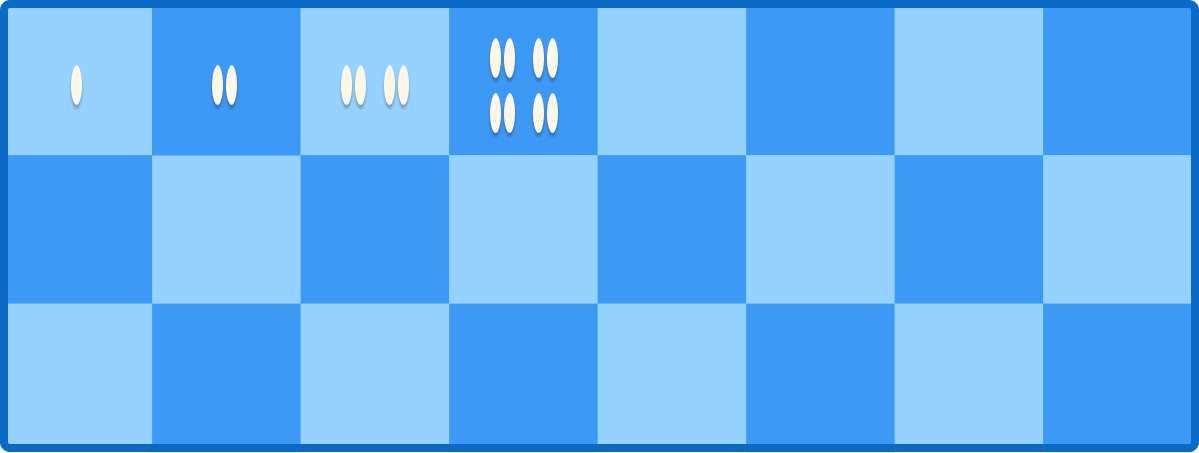
Chess & Rice Grain

Algebra Level 1

A girl puts $1$ grain of rice in the first square of an 8 by 8 chess board. In the subsequent square, she puts twice that of the previous square, and she continues until she fills all the squares.

How many total grains does she need?

\binom{64}{2}

2^{64}-1

64!

2^{63}-1

8 solutions

Khang Nguyen Thanh
Aug 7, 2015

The sum of grains he need is:

$A=1+2+2^2+2^3+\ldots+2^{63}\qquad \quad(1)$

Multiplying both side by 2, we get:

$2A=2+2^2+2^3+2^4+\ldots+2^{64}\qquad\; (2)$ .

From $(1)$ and $(2)$ we have: $A=2A-A=\boxed{2^{64}-1}$ .

Let x be the square you are on, and f(x) be the number of grains of rice on that square. Could you integrate the function: $f(x) = 2^{x-1}$ within the limits of x = 0 and x = 64 to give you the sum of grains of rice needed?

Conor Straub - 5 years, 10 months ago

The limits should be x=1 to x=64.

Integrating 2^{x-1} gives 2^{x-1}/In2,

And after inserting the limits, it gives: 2^{63}/In2 - 2^{0}/In2

= [2^{63}-1]/In2

But integrating won't give the right answer as x (the square number) only takes discrete values and is not continuous from x=1 to x=64, for example: you can't have a square number- 45.778, even if it is within the range.

So, integration cannot be used. The number of rice grains on squares of chess board from square 1 to square 64 forms a geometrical sequence: 1, 2, 4, 8,......

The first term (a) is 1, common ratio (r) is 2 and number of squares (n) is 64.

The geometric series summation formula is: a(1-r^{n}) / (1-r)

Inserting a, r and n into that formula gives (1-2^{64})/ (-1) = 2^{64} -1.

Stuti Malik - 5 years, 10 months ago

That's a great response, thanks! Appreciate the amount of detail!

Conor Straub - 5 years, 10 months ago

None of these solutions work. There soon would not be enough room in the each square to accommodate the requisite number of rice grains. The actual number would be far smaller than the theoretical number.

Daniel Langstaff - 3 years, 5 months ago

This is none other than the famous Wheat and Chessboard Problem . In a nutshell, the story goes like... the inventor of chess after presenting his ingenuity before the king asked for his gift in a process as described above. The mathematically ignorant king thought it was nothing as compared to his enormous wealth but soon became crazy and probably abdicated out of shame!

(There are many versions of the story, this is the one I know)

Shubhrajit Sadhukhan - 8 months, 3 weeks ago

A Former Brilliant Member
Jun 15, 2017

The common ratio is $r=\dfrac{2}{1}=\dfrac{4}{2}=2$

The sum of terms of a GP is given by

$s=\dfrac{a_1-a_1r^n}{1-r}$ $\implies$ $s=\dfrac{1-1(2^{64})}{1-2}=\dfrac{1-2^{64}}{-1}=-(1-2^{64})=-1+2^{64}=$ $\boxed{2^{64}-1}$

Bob Raphael
Sep 9, 2015

No solution needed. It was the only answer that made sense. 64! was clearly wrong as was (64 2). Recognizing that there are 64 squares with a base of 2 and a single square with one grain made the answer clear.

Shreeprada Hegde
Aug 29, 2015

The sequence of putting the grains in the chess board is 1,2,4,8,......... It is in GP.Total boxes in chess board is 64. So total grains =a(r raise to n -1)/r-1 Here r = 2,a=1 Therefore, total grains=2raise to 64 -1

U.N. Owen
Aug 29, 2015

I remember this problem from a Brazilian recreational mathematics book. If anyone's curious, 2^64 - 1 = 18 446 744 073 709 551 615.

Don Weingarten
Feb 2, 2019

There are 64 squares on a chessboard, and all but the first square has a power of 2 grains. Thus the answer is 2 to the 64th power minus 1 grain.

Ervyn Manuyag
Nov 20, 2018

Bcuz the pattern is 2^x-1 and there is 8x8=64

Sadasiva Panicker
Aug 23, 2015

Sn = ax(r^n-1) = 1x(2^64 - 1)

Chess & Rice Grain

8 solutions

0 pending reports