Child Labor #3

Computer Science Level 4

Find the least value of $n$ such that $1!\times2!\times3!\times\ldots\times n!$ has more than 2015 trailing zeros.

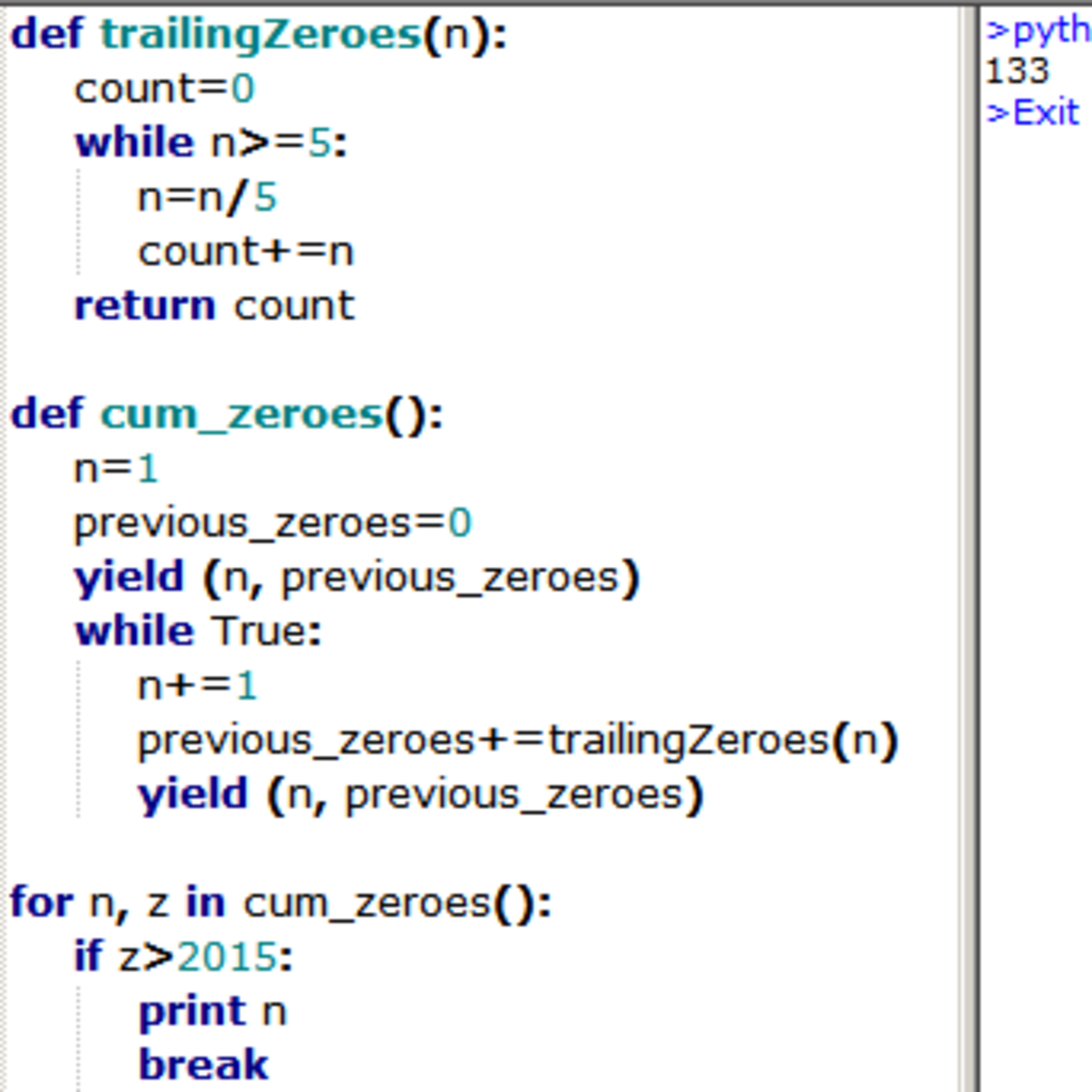
The answer is 133.

6 solutions

Roel Baars
Jul 1, 2015

Mathematica

1
2
3

n = 1;
 While[Mod[Product[i!, {i, 1, n}], 10^2015] != 0, n++]
n

Here 's a C++ solution. Although, I suspect that this problem can be done by number-theoretic methods without relying on programming.

Prasun Biswas - 5 years, 10 months ago

Yes it's possible but tedious. You can start by bounding it to show the answer is in between 100 and 150, then use bisection method. Even then, it's tedious and it's best to leave it to a computer.

Pi Han Goh - 5 years, 10 months ago

Bill Bell
Jul 7, 2015

Uses repeated division by fives, essentially. Does not calculate factorials.

Arulx Z
Jul 1, 2015

import math
prod = 1
num = 0
while len(str(prod)) - len(str(prod).rstrip('0')) <= 2015:
    num += 1
    prod *= math.factorial(num)
print num

Moderator note:

Good, standard solution.

Vincent Miller Moral
Jun 30, 2015

#include <iostream>

int numZeroes( int n );

int main()
{
    int ctr = 0;
    int i;

    for( i=5 ; ctr<=2015 ; i++ )
        ctr += numZeroes(i);

    std::cout << i-1 << " " << ctr << std::endl;
    return 0;
}

int numZeroes( int n )
{
    int ctr = 0;

    for( int i=5 ; i<=n ; i*=5 )
        ctr += n/i;
    return ctr;    
}

Nathanael Case
Jul 18, 2015

C/C++

int factorialZeros(int a) { // counts the trailing zeros in a!
    int n=1;
    int zeros = 0;
    while (a/atotheb(5,n)!=0) {
        zeros +=a/pow(5,n);
        n++;
    }
    return zeros;
}


int main() {
    int zeros = 0,n=0;
    while (zeros<2015) {
        n++;
        zeros += factorialZeros(n); 
    }
    cout << n << endl; //gives n = 133
    cout << zeros << endl; //which has 2033 trailing zeros
    return 0;
}

Brock Brown
Jul 1, 2015

Python 3.3:

from math import factorial
n = 1
product = 1
def trailing_zeroes(n):
    s = str(n)
    index = len(s) - 1
    count = 0
    while s[index] == '0':
        count += 1
        index -= 1
    return count
while trailing_zeroes(product) <= 2015:
    n += 1
    product *= factorial(n)
print("Answer:", n)

Child Labor #3

The answer is 133.

6 solutions

Moderator note:

0 pending reports