Child Labor #3
Find the least value of n such that 1 ! × 2 ! × 3 ! × … × n ! has more than 2015 trailing zeros.
The answer is 133.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Here 's a C++ solution. Although, I suspect that this problem can be done by number-theoretic methods without relying on programming.
Log in to reply
Yes it's possible but tedious. You can start by bounding it to show the answer is in between 100 and 150, then use bisection method. Even then, it's tedious and it's best to leave it to a computer.
Uses repeated division by fives, essentially. Does not calculate factorials.
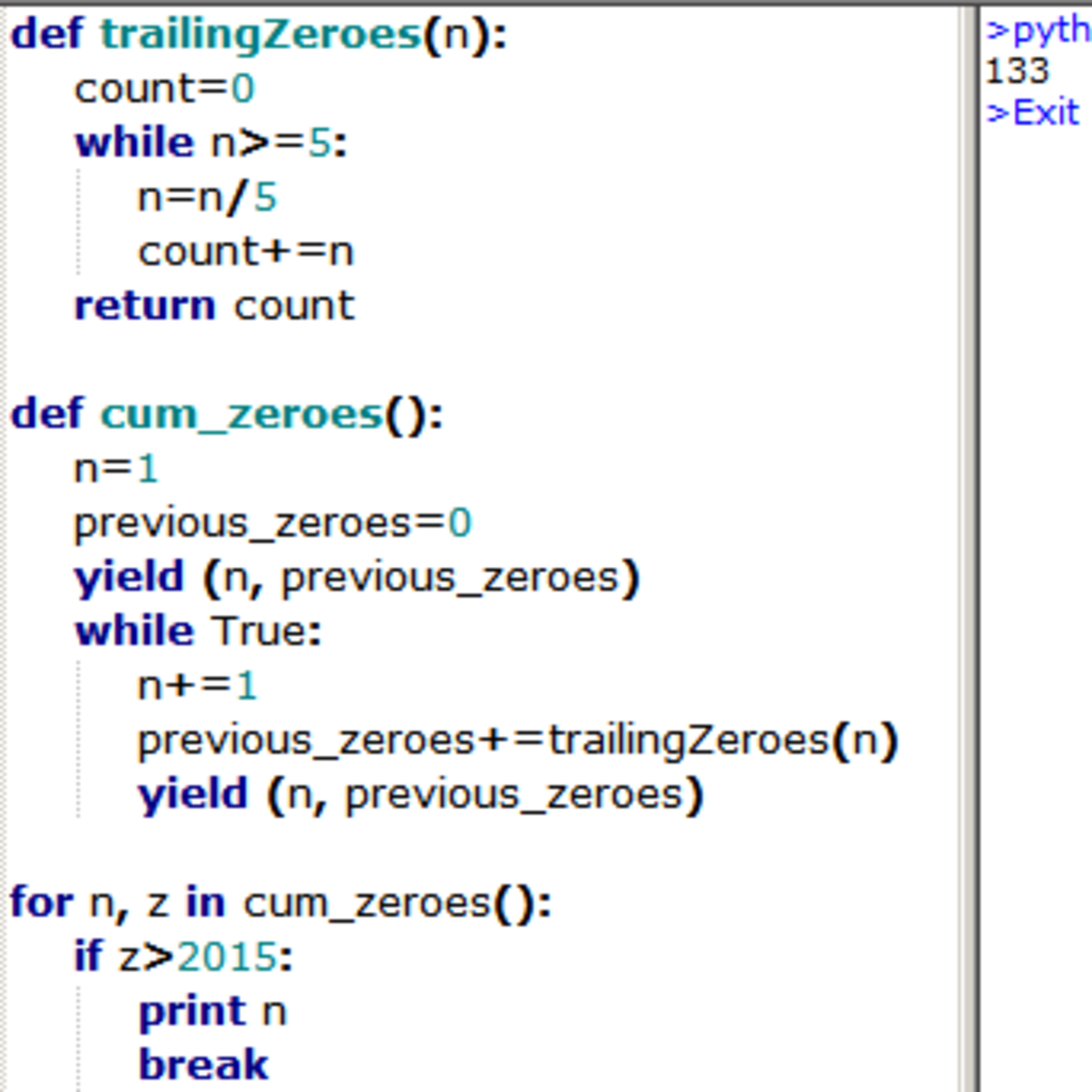
1 2 3 4 5 6 7 |
|
Moderator note:
Good, standard solution.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
C/C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
Python 3.3:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
Mathematica