Children sliding down a hill

Let the velocity of the child rotates by and angle $\theta$ and decreases to $v$ in time $t$ . It is acted upon by the two forces in the plane of the inclined plane. One is the gravitational force $F$ and the other is the friction force.

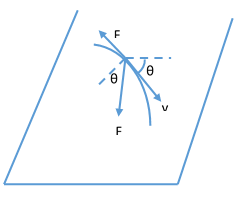
It is being stated in the problem that the child will move down at a constant speed if he is pushed slightly down the hill. This implies that the friction force is equal to the gravitational pull down the incline. Although, in this case, the velocity of the child is not down the incline, therefore, the friction although will be equal to $F$ but will not be opposite to the gravitational pull. Rather, it will be opposite to the instantaneous velocity.

Now, the net force perpendicular to the velocity is written as, $F \cos \theta = mv \frac{d\theta} {dt}.$ The force opposite to velocity can be written as, $F-F \sin \theta = - m \frac{dv}{dt}.$ Dividing the two equations, we will get $\frac{{\cos \theta }}{{1 - \sin \theta }} = - \frac{{vd\theta }}{{dv}}$ $- \int_1^{v_f} {\left( {\frac{1}{v}} \right) \, dv} = \int_0^{\pi/2} {\frac{{1 - \sin \theta }}{{\cos \theta }} \, d\theta }.$ Solving this, we will get $v_f= \boxed{0.5} ms^{-1}.$

Let $F$ be the downhill component of the gravitational force; according to the given above, this is equal to the frictional force.

At any given moment, let $\theta$ be the angle between the sled and the vertical.

Tangentially, $ma_{tan} = F_{g,tan} - F_f = F\cos\theta - F.$

In the downhill direction, $ma_y = F_g + F_{f,y} = F - F\cos\theta.$

It follows that $a_{tan} + a_y = 0$ , or $0 = \frac{dv}{dt} + \frac{d(v\cos\theta)}{dt} = \frac{dv}{dt}(1+\cos\theta) - v\sin\theta\frac {d\theta}{dt} = \frac{d}{dt}v(1+\cos\theta).$ Therefore $v(1+\cos\theta)$ is a constant of the motion.

$v_f(1+\cos\theta_f) = v_i(1+\cos\theta_i)\ \therefore\ v_f(1+1) = v_i(1+0)\ \therefore\ v_f = \boxed{1/2}.$