Choco Balls Riddle
A famous chocolate shop sells the delicate Choco balls in 3 different packages: a small square box of 9 Choco balls, a middle hexagonal box of 1 4 , and a large triangular box of 2 1 .
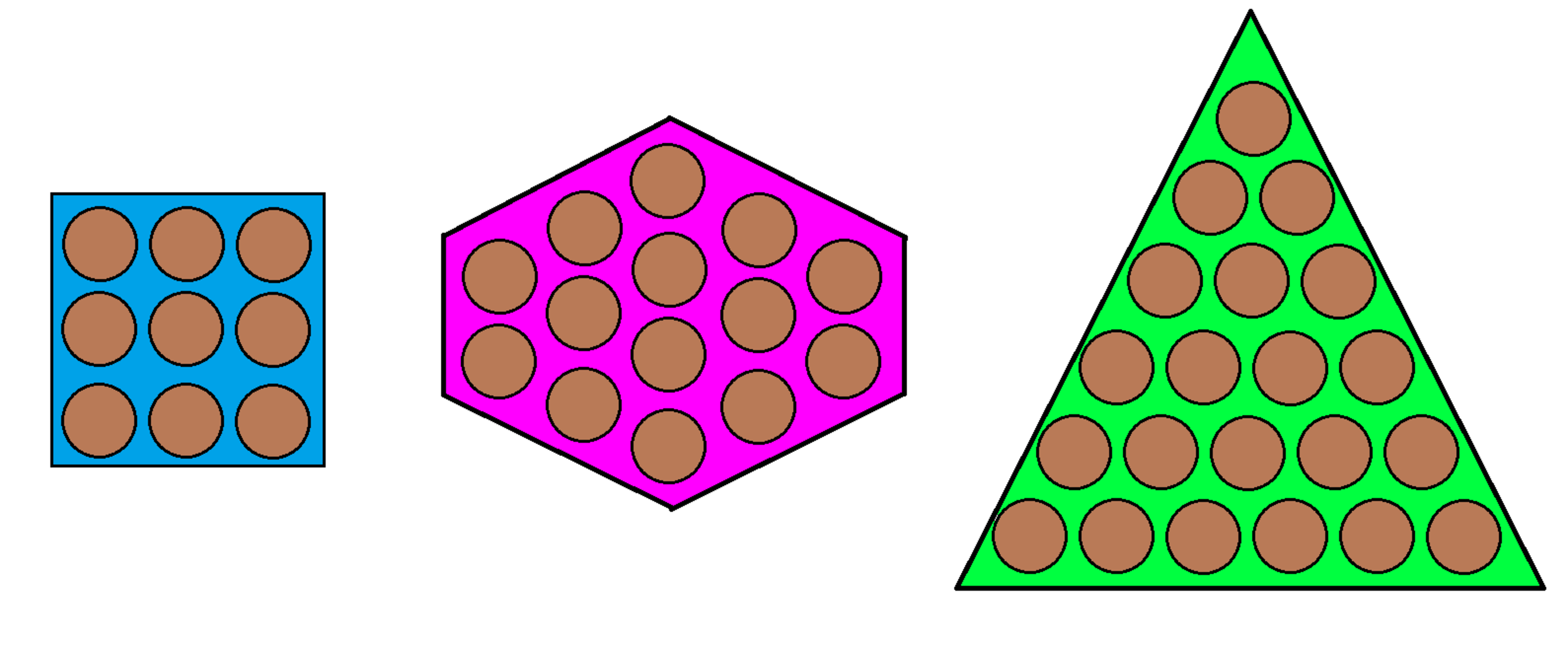
If you would like exactly 8 5 Choco balls, how many boxes in total would you need to buy?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The remainder after dividing 85 by 7 is 1.
8 5 m o d 7 = 1
The remainder after dividing 9 by 7 is 2.
9 m o d 7 = 2
(The other boxed do not contribute, since 14 and 21 are divisible by 7)
It takes multiplying by 4 to get the right remainder:
9 × 4 m o d 7 = 2 × 4 m o d 7 = 8 m o d 7 = 1
After taking off 4 boxed with 9 chocolates each, we are left with 49 to distribute between boxes size 2 × 7 and 3 × 7 .
4 9 / 7 = 7
7 distributed in chunks of 2 or 3 can be written as 7 = 2 + 2 + 3 , two boxes of 14 each, one with 21.
Let , number of square boxes, hexagonal boxes and triangular boxes are x , y , z respectively.
Then 9 x + 1 4 y + 2 1 z = 8 5 7 ( 2 y + 3 z ) = 8 5 − 9 x
It implies 7 ∣ 8 5 − 9 x ⟹ 7 ∣ 1 − 9 x ⟹ 7 ∣ 1 − 2 x
So, appropriate solution of x = 4 .There are many many other solutions but this will cross the value 8 5
7 ( 2 y + 3 z ) = 8 5 − 3 6 = 4 9 2 y + 3 z = 7
Here the only solution is y = 2 ; z = 1
So, total boxes required to buy 4 + 2 + 1 = 7
Since 8 5 is not a multiple of 7 or 9 , this amount can not be put in terms of one type of box alone. Neither can it be put in terms of 1 4 and 2 1 because it would need to be a multiple of 7 . Thus, the small box must be involved no matter what.
Then suppose 8 5 ≡ 7 n ( m o d 9 ) .
Then 8 5 ≡ 4 ≡ 7 ⋅ 7 ≡ 4 9 ( m o d 9 ) .
Thus, n = 7 , and there is only one way to put 4 9 Choco balls in terms of the bigger boxes:
4 9 = ( 4 ⋅ 7 ) + ( 3 ⋅ 7 ) = 2 ⋅ 1 4 + 2 1 .
Hence, we need to buy 2 middle boxes and 1 large box, which leaves us 4 small boxes, for 8 5 − 4 9 = 3 6 = 4 ⋅ 9 .
Finally, the number of boxes = 4 + 2 + 1 = 7 .