Chocolate Breaker

Relevant wiki: Linearity of Expectation

Let $m,\mu,M$ be the smallest, middle and largest lengths created. Then $m + \mu + M = 1$ , so that $\mathbb{E}[m] + \mathbb{E}[\mu] + \mathbb{E}[M] \; = \; 1$ Suppose that the two breaks in a bar take places at points $x$ and $y$ where $x,y$ are independently and uniformly distributed on $[0,1]$ .

The smallest length $m$ can only take values between $0$ and $\tfrac13$ . If $0 < u < \tfrac13$ , we have $m \le u$ precisely when either $x \le u$ , $y \le u$ , $x \ge 1-u$ , $y \ge 1-u$ or else $|x-y| \le u$ . Considering the first diagram we see that $m \le u$ precisely when $(x,y)$ lies outside the yellow region. Thus $F_m(u) \; = \; \mathbb{P}[m \le u] \; = \; 1 - (1 - 3u)^2 \hspace{2cm} 0 \le u \le \tfrac13$ so that $m$ has probability density function $f_m(u) \; = \; \left\{ \begin{array}{lll} 6(1-3u) & \hspace{1cm} & 0 \le u \le \tfrac13 \\ 0 & & \mbox{o.w.} \end{array} \right.$ Thus we have $\mathbb{E}[m] \; = \; \int_0^{\frac13} 6u(1-3u)\,du \; = \; \tfrac19$

The largest length $M$ can only take values between $\tfrac13$ and $1$ . If $\tfrac13 < u < 1$ we have $M \ge u$ when either both $x,y \le 1-u$ , both $x,y \ge u$ or else $|x-y| \ge u$ . Looking at the second and third pictures, this means that $M \le u$ when $(x,y)$ lies in the indicated yellow regions, and hence $F_M(u) \; = \; \mathbb{P}[M \le u] \; = \; \left\{ \begin{array}{lll} (3u-1)^2 & \hspace{1cm} & \tfrac13 < u < \tfrac12 \\ 1 - 3(1-u)^2 & & \tfrac12 < u < 1 \end{array}\right.$ so that $M$ has probability density function $f_M(u) \; =\; \left\{ \begin{array}{lll} 6(3u-1) & \hspace{1cm} & \tfrac13 < u < \tfrac12 \\ 6(1-u) & & \tfrac12 < u < 1 \\ 0 & & \mbox{o.w.} \end{array} \right.$ so that $\mathbb{E}[M] \; = \; \int_{\frac13}^{\frac12} 6u(3u-1)\,du + \int_{\frac12}^1 6u(1-u)\,du \; = \; \tfrac{11}{18}$ and hence $\mathbb{E}[\mu] \; = \; 1 - \tfrac19 - \tfrac{11}{18} \; =\; \tfrac{5}{18}$ and so $\mathbb{E}[m] \times \mathbb{E}[\mu] \times \mathbb{E}[M] \; = \; \tfrac19 \times \tfrac{5}{18} \times \tfrac{11}{18} \; = \; \tfrac{55}{2916}$ making the answer $55 + 2916 = \boxed{2971}$ .

Relevant wiki: Geometric Probability

Let $S$ , $M$ , and $L$ be random variables that represent lengths of the smallest, medium-sized and largest piece, and let $X$ and $Y$ represent breaking points. Without loss of generality, we can say $X < Y$ and reduce the probability space of possible breaking outcomes $(X, Y)$ to the region above the line $Y = X$ . Mind that this effectively doubles any probability calculation (see Conditional Probability ).

Let us first say that the smallest piece occurs on the left, so $S = X$ . You can adapt the logic below for the middle ( $S = Y - X$ ) and right ( $S = 1 - Y$ ) place, and you will see that i) the chance that the smallest piece is anywhere along the stick is even, and ii) no matter where it is, the average length is the same. If the smallest piece occurs on the left though, the following holds:

$\Big( X < Y - X \Big) \land \Big( X < 1 - Y \Big)$

This region is depicted dark green on the left. Since $\mathbb{E}[S] = \mathbb{E}[X]$ , we have to find the x-coordinate of the geometric center of that triangle. In a general triangle, center is at one third along the median, which means $E[S] = \frac{1}{9}$ in this case. Result is the same if the smallest piece occurs in the middle (lighter green) or on the right (still lighter green). You may want to verify this.

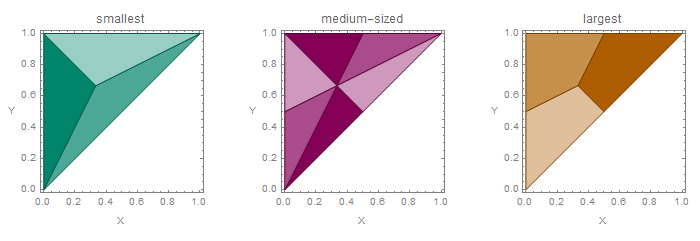
How about the medium-sized piece? Let it first occur on the left. This means $M = X$ and:

$\Big( X > Y - X \land X < 1 - Y \Big) \lor \Big( X < Y - X \land X > 1 - Y \Big)$

This is depicted dark violet in the middle. Lighter region denotes the middle piece, and still lighter region denotes the right piece. Calculating the x-coordinate of the centroid of the dark violet region (comprising of two disjoint parts) determines $\mathbb{E}[M] = \frac{5}{18}$ . Note that in the case of the middle piece, one should calculate both centroid coordinates since then $\mathbb{E}[M] = \mathbb{E}[Y - X]$ . But one would be better off, as Mark Hennings has noted in his solution, finding $\mathbb{E}[L]$ first and using the fact that there are exactly three pieces, so $M = 1 - (L + S)$ , and by linearity of expectation $\mathbb{E}[M] = 1 - (\mathbb{E}[L] + \mathbb{E}[S])$ . In short, find centroid for each of any two pieces at any place, and use identity for the third piece.

My solution is not significantly different from the others posted here. Note that a bit of symmetry can be added by letting $x$ = length of left piece, $y$ = length of right piece. The possible situations are then limited by $x + y \leq 1$ , and without loss of generality we can limit ourselves to $x < y$ .

I, too, did some graphing. The red, blue, green lines correspond to the smallest, medium, and longest piece. Enjoy.

Let $x$ be the length of the small chocolate piece and $y$ be the length of the medium chocolate piece. The following are constraints on $x$ and $y$ .

• $0 < x < 1$ and $0 < y < 1$

• $x \leq y$ . This ensures that the medium piece is at least as large as the small piece.

• $y \leq 1 - x - y$ . This ensures that the large piece is at least as large as the medium piece.

Through some algebra, we conclude that the region on the xy-plane which satisfies these constraints are $x\le y\le\frac{1-x}{2}\left\{\frac{1}{3}\ge x\ge0\right\}$ . The region is a triangle with base $\frac{1}{2}$ , height $\frac{1}{3}$ , and area $A = \frac{1}{12}$ .

Let $s = E[x]$ , $m = E[y]$ , $l = E[1 - x - y] = 1 - E[x] - E[y]$ . Then $s = \displaystyle \frac{\int_{0}^{\frac{1}{3}}\int_{x}^{\frac{1-x}{2}}xdydx}{A} = \frac{1}{9}$ , $m = \displaystyle \frac{\int_{0}^{\frac{1}{3}}\int_{x}^{\frac{1-x}{2}}ydydx}{A} = \frac{5}{18}$ , and $\displaystyle l = 1 - s - m = \frac{11}{18}$ . Finally, $s \cdot m \cdot l = \frac{55}{2916}$ meaning that the answer to the problem is $55 + 2916 = \boxed{2971}$