Chocolate mania (mechanics +trigonometry)

Classical Mechanics Level 5

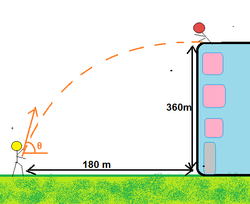Cody is this time throwing a chocolate from the ground and the lady \color{#D61F06}{\text{lady}} is on the top of the building to catch it.

The point from where Cody throws the chocolate is 180 m 180\, \text{m} away from the building and building is 360 m 360\,\text{m} tall.

Given that when the lady \color{#D61F06}{\text{lady}} caught the chocolate, it was travelling horizontally (vertical velocity 0 m/s 0\,\text{m/s} ) and Cody had thrown the chocolate with the initial velocity making an angle θ \theta with the horizontal, then find the value of

tan ⁡ θ × tan ⁡ ( 6 0 ∘ − θ ) × tan ⁡ ( 6 0 ∘ + θ ) \tan \theta \times \tan (60^\circ -\theta) \times \tan(60^\circ +\theta)

This value can be written as a b \dfrac{a}{b} for coprime positive integers a a and b b . then find the value of a + b a+b .

Details : In this problem, you don't need the initial velocity at all, neither the value of acceleration due to gravity.


The answer is 99.

Aditya Raut by Aditya Raut , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Aditya Raut
Jun 18, 2014

As the chocolate was travelling horizontally when it reached the lady , it is at the maximum height reached.

The formula for maximum height is

H m a x = u 2 s i n 2 θ 2 g H_{max} = \dfrac{u^2 sin^2\theta}{2g} .... u u is initial velocity, g g is acceleration due to gravity...

and also , it has covered half the distance it would , if the building wasn't there. The horizontal distance Range is

R = u 2 s i n 2 θ g R= \dfrac{u^2 sin2\theta}{g} hence in this case, the distance is R 2 = u 2 s i n 2 θ 2 g \frac{R}{2} = \dfrac{u^2 sin2\theta}{2g}

The ratio , from given values is H m a x R / 2 = u 2 s i n 2 θ 2 g u 2 s i n 2 θ 2 g \dfrac{H_{max}}{R/2} = \dfrac{\dfrac{u^2 sin^2\theta}{2g}}{\dfrac{u^2 sin2\theta}{2g}}

360 180 = s i n θ 2 c o s θ = t a n θ 2 \dfrac{360}{180} = \dfrac{sin\theta}{2 cos\theta} = \dfrac{tan\theta}{2}

Thus we get that t a n θ = 4 tan\theta =4

Asked expression is actually

t a n θ t a n ( 6 0 ∘ + θ ) t a n ( 6 0 ∘ − θ ) = t a n 3 θ = 3 t a n θ − t a n 3 θ 1 − 3 t a n 2 θ tan\theta tan(60^\circ +\theta)tan(60^\circ-\theta) = tan3\theta = \dfrac{3tan\theta - tan^3\theta}{1-3tan^2\theta}

= 12 − 64 1 − 48 = − 52 − 47 = 52 47 = \dfrac{12-64}{1-48} = \dfrac{-52}{-47} = \dfrac{52}{47}

hence answer is 52 + 47 = 99 52+47 = \boxed{99}

22 Helpful 0 Interesting 0 Brilliant 0 Confused

The relation between maximum height( H ) attained by a projectile and it's range( R ) is:

H = R 4 tan ⁡ θ H=\frac { R }{ 4 } \tan { \theta }

Substituting the values over there you can easily get tan ⁡ θ = 4 \tan { \theta } =4 . Not much difference but it seriously reduces the number of steps needed and saves time.

Siddharth Singh - 6 years, 11 months ago

Log in to reply

That's true but not all people know about how that was derived, so I added this solution so that everyone tries to understand how the formula was obtained !

Aditya Raut - 6 years, 11 months ago

There is another general formula for projectile motion. H = xtanθ( 1 - x/R ). If you put H = 360, x = 180 and R = 360, you get tanθ = 4.

R.l. Bhat - 6 years, 11 months ago

woah amazing solution nicely done. thumbs up @adyita

Mardokay Mosazghi - 6 years, 11 months ago

i was stuck with tan3A. where did you get that transformatoin? i surprized that i really close :P

Hafizh Ahsan Permana - 6 years, 11 months ago

Log in to reply

It's an identity,you may try to prove it ! But for that, you need to know some more identities and the form of tan3A in for of tanA

Aditya Raut - 6 years, 11 months ago

How did you get the three part trig ? Tan sum of angle is standard.

Niranjan Khanderia - 6 years, 11 months ago

Log in to reply

I jsut used an Identity buddy :)

Aditya Raut - 6 years, 11 months ago

Directly the relation between range and the trajectory can be used to give us tan ⁡ θ \tan { \theta }

y = x tan ⁡ ϑ ( 1 − x R ) y=x\tan { \vartheta } (1-\frac { x }{ R } ) ;y=360, x=180, r=range=2 × \times 180=360

*Note this equation can be obtained by taking x tan ⁡ θ \tan { \theta } common out of the usual trajectory equation

Gunraj Singh - 6 years, 10 months ago

Thank you for the very nice solution... =)

I got stuck in simplifying the expression... But I was just one step away... But yeah... Thanks!!! =D

Bon Leif Amalla - 6 years, 10 months ago

I did it in a mathematical way: I created a parabola function that would represent the path of the chocolate (the lower left corner of the building is the origin), which is f ( x ) = − 1 90 x 2 + 360 f(x)=-\frac{1}{90}x^2+360 . Then, according to Wikipedia , the line, the angle of which is θ \theta w.r.t the x axis, is r ( x ) r(x) , where f ( x ) = − 1 90 ( x + 180 ) 2 + r ( x ) f(x)=-\frac{1}{90}(x+180)^2+r(x) . In this case, r ( x ) = 4 x + 720 r(x)=4x+720 , which means tan ⁡ θ = 720 180 = 4 \tan\theta = \frac{720}{180}=4 , and the rest is the same as you did. I don't know much about physics and am not sure about the physics formulas in your solution, but this solution sufficed. How come the path appeared to have been a perfect parabola? Interesting.

mathh mathh - 6 years, 10 months ago

Log in to reply

By equations of motion derived from Newton's laws, this parabolic shape is explained.

The x x displacement is an equation in t t of degree 1 1 as no acceleration is there in horizontal direction, but y y displacement is a quadratic function of t t (time) , so it's parabolic movement in all. (as we have in graph of y = x 2 y=x^2 , you need the 2nd power of X X to have a form similar to Y Y , this means the path has to be a parabola when movement is considered to be for both x x and y y directions simultaneously

Aditya Raut - 6 years, 10 months ago

First write the equations of the movement. Note that i and j, are the horizontal and vertical unit vectors respectively. a = − g i a = -g i

V o = V o cos ⁡ θ i + V o sin ⁡ θ j Vo = Vo\cos\theta i + Vo\sin\theta j

The integral of the acceleration is the velocity

V = ( − g t + V o sin ⁡ θ ) j + V o cos ⁡ θ i V = ( -gt + Vo\sin\theta)j + Vo\cos\theta i

The integral of the Velocity is the position of the object. If the origin is the point of Cody when just threw the chocolate:

r = ( − g t 2 / 2 + V o t sin ⁡ θ ) j + V o t cos ⁡ θ i r = ( -gt^2 / 2 + Vot\sin\theta)j + Vot\cos\theta i

Puting the conditions inside our equations:

V o t cos ⁡ θ = 180....... I Vo t \cos\theta = 180 ....... I (The chocolate must travel a distance of 180 meters in the horizontal)

− g t + V o sin ⁡ θ = 0........ I I -gt + Vo\sin\theta = 0 ........ II (The lady must catch the chocolate when it is travelling horizontally)

− g t 2 / 2 + V o t sin ⁡ θ = 360..... I I I -gt^2 / 2+ Vot\sin\theta = 360 ..... III (The chocolate should reach the top of the tower)

Now we should reduce an equation to terms of tan ⁡ θ \tan\theta , and get that tan ⁡ θ = 4 \tan\theta = 4

Working in our answer...

tan ⁡ ( 60 ° − θ ) = s q r t ( 3 ) − 4 1 + 4 s q r t ( 3 ) \tan(60° - \theta) = \frac{ sqrt(3)- 4 }{1 + 4sqrt(3)}

tan ⁡ ( 60 ° + θ ) = s q r t ( 3 ) + 4 1 − 4 s q r t ( 3 ) \tan(60° + \theta) = \frac{ sqrt(3)+ 4 }{1 - 4sqrt(3)}

Multiplying tan ⁡ ( 60 ° + θ ) \tan(60° + \theta) and tan ⁡ ( 60 ° − θ ) \tan(60° - \theta) we have a difference of squares.

Thus: a b = 52 47 = > a + b = 99 \frac{a}{b} = \frac{52}{47} => a+b=99

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Average up velocity when final velocity = 0 is V * sin(thita)/2.

Ratio H/R={ [ V * sin(thita) * t ]./.2 }./.{ V * cos(thita) * t } =tan(thita)./.2=360/180. .. tan(thita) = 4. ........... tan(60) = sqrt(3).

Exp. =4 * { [tan(60) - tan(thita)] ./.[ 1 + tan(60) * tan(thita)] }
* { [tan(60) + tan(thita)] ./.[ 1 - tan(60) * tan(thita)] }
=4 * { [sqrt(3) - 4]./.[1 + sqrt(3) * 4] } * { [sqrt(3) + 4]./.[1 - sqrt(3) * 4] }
=4 * {3 - 16}./.{1 - 48} = 52./.47.........52 + 47 = 99.


2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...