Chomp again

Probability Level 5

Refer to Chomp for the rules of this tasty game.

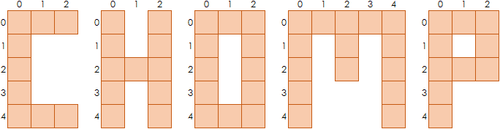
Knowing that the game on rectangular boards is rigged, the players are now playing with irregular boards as depicted on the picture. With optimal play, who wins each game? Answer $1$ if the first player wins and $2$ if the second player wins. String all five digits together. Thus, if the first player wins on all boards but the M, your answer should be $11121$ .

Remember that each player must select a piece; they cannot select an empty square! So on the P, it's illegal to move on $(1,1)$ to capture the three pieces to the right and below it, as $(1,1)$ is not a piece.

The answer is 11112.

1 solution

Ivan Koswara
Jan 6, 2015

The answer is $11112$ ; the first player wins on all but the P.

Observe how the first four boards have a lower-right piece on $(4,2)$ . This is all it needs for the first player to win, by using the same strategy-stealing argument as in the rectangular boards.

For the P, things are harder; my solution proves that none of the available moves win for the first player. First, playing on $(0,0)$ clearly loses; playing on $(0,1)$ or $(1,0)$ also loses as it leaves a rectangular block.

Next, we will show that whenever the board satisfies a) along the main diagonal, $(0,0)$ and only that is in the board (so $(x,x)$ is not in the board for $x \neq 0$ ), and b) the board is symmetric along the main diagonal, the second player wins. The strategy is simply by playing symmetrically. To see why this works, observe that the first player can either play on $(0,0)$ which loses instantly, or play on $(r,c)$ with $r \neq c$ , in which the second player can play on $(c,r)$ to re-establish symmetry.

What does this prove? If the first player plays on $(2,0)$ , the second player can respond by playing on $(0,2)$ to produce a symmetrical board (a $2 \times 2$ square with lower-right corner removed). Of course, similarly, if the first player plays on $(0,2)$ , the second player responds on $(2,0)$ . Next, if the first player plays on $(3,0)$ , the second player plays on $(2,2)$ , and vice versa, to produce another symmetric board.

Now things get more complicated. If the first player plays on $(2,1)$ , the winning response is to play on $(4,0)$ , and vice versa. One can see in the following image; in the third diagram, if the first player plays on any of the squares with an arrow, then the second player can play on its pair to produce symmetry, and of course playing on $(0,0)$ is suicidal.

The last move by the first player is $(1,2)$ , where again the winning response is $(4,0)$ . In fact, the third diagram is strikingly similar:

Thus whatever move the first player plays, there is a winning response for the second player. Thus it's second-player win.

Chomp again

The answer is 11112.

1 solution

0 pending reports