Chomp

Probability Level 4

The game Chomp is a game played by two players with a piece of "chocolate", which can be modeled as a set of squares $(r_i, c_i)$ where $r_i, c_i \ge 0$ for all squares. Starting from the first player, each player in turn selects one square $(r_p, c_p)$ and eats (removes) it along with all pieces with coordinates at least equal to it; that is, all squares $(r,c)$ where $r \ge r_p, c \ge c_p$ . The player that makes the last move loses .

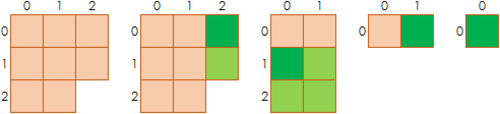
The picture shows a sample game on a $3 \times 3$ board with lower-right piece removed (first diagram). The first player makes the move $(0,2)$ , eating it along with the piece below it (second diagram). The second player makes the move $(1,0)$ , which leaves a $1 \times 2$ rectangle (third diagram). The first player then moves on $(0,1)$ , forcing the second player to take the remaining block and thus lose.

Suppose the players play a game of Chomp on an $m \times n$ rectangular block of chocolate. Among all such games where $1 \le m,n \le 10$ , how many games are won by the first player?

The answer is 99.

1 solution

Ivan Koswara
Jan 6, 2015

For the exceptional case $1 \times 1$ block, the first player loses. In all other cases, the first player wins.

First, note that the game must end (since one piece disappears after every move, and there are only finitely many pieces), and the game cannot end in a tie (there must be someone that will make the last move and hence loses).

Now, we will show the existence of a strategy for the first player by strategy-stealing argument . Suppose the second player has a winning strategy. Then if the first player plays on $(m-1, n-1)$ , the second player wins by playing on $(r_w, c_w)$ . But then the first player could have started by playing on $(r_w, c_w)$ immediately; now the situation is identical to the above, but with reversed players, thus making the first player has the win, contradiction. So the second player cannot have a winning strategy, and thus the first player wins instead.

In the example above, we assume $m=n=3$ . Suppose the second player has a winning strategy. Then when the first player plays on $(2,2)$ , the second player wins by playing on some square, for example $(1,1)$ . But then the first player could have played on $(1,1)$ immediately to win; this leaves the exact same situation but with players reversed.

The reason why the above breaks down when $m=n=1$ is the assumption that the second player wins by playing . On the $1 \times 1$ board, the second player wins immediately, without need to play any other move, and thus the first player cannot "steal" this.

Chomp

The answer is 99.

1 solution

0 pending reports