Chomping Cow

By constructing arcs we can see where the cow is able to graze. At the corners, the rope is cut off at a certain point acting as a new anchor point for the rope, resulting in the 15m and 40m quadrants.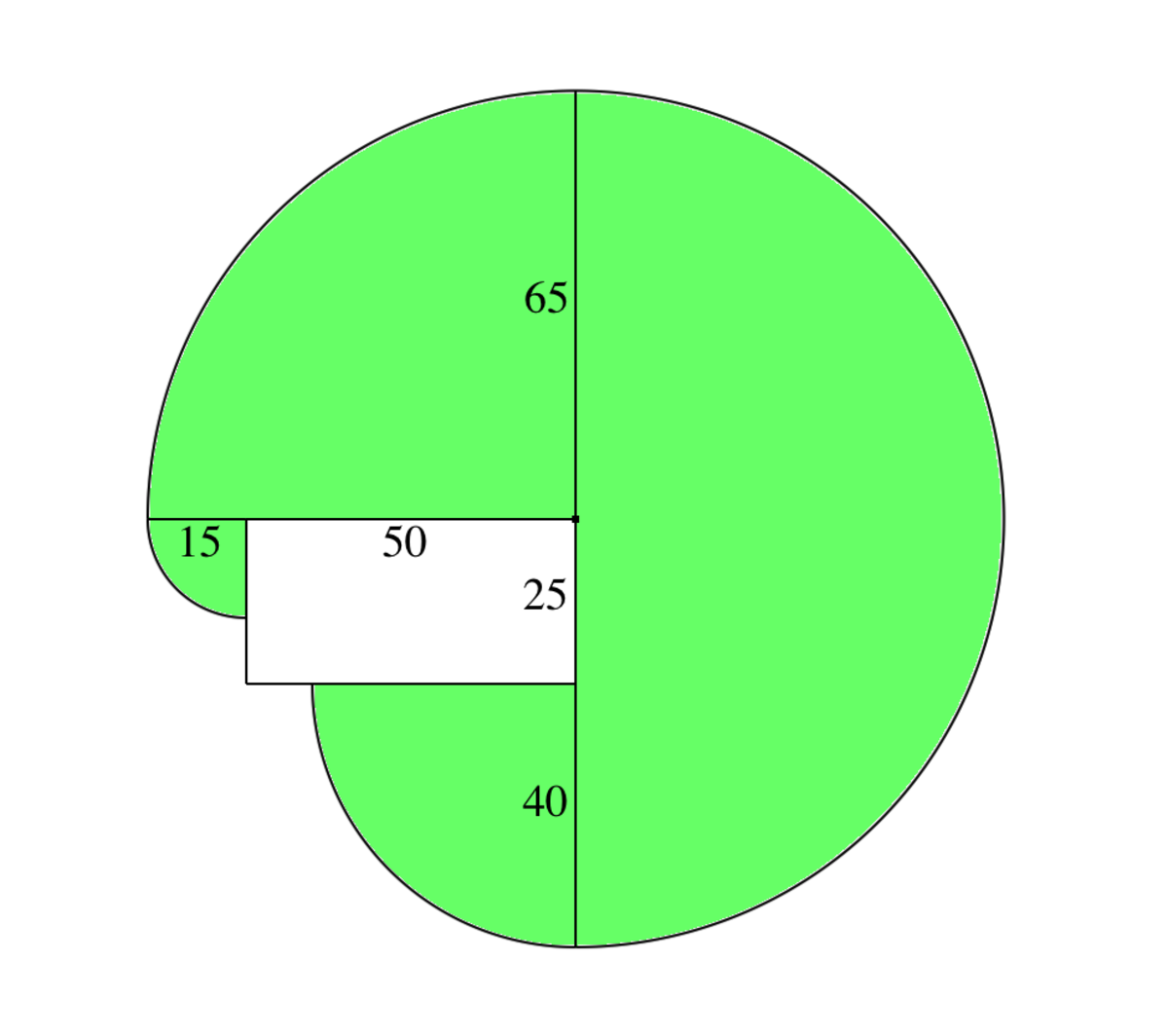 Finding the area of each of these sectors we get: $\begin{aligned}A=\frac{3}{4}\pi65^2+\frac{1}{4}\pi15^2+\frac{1}{4}\pi40^2\\ =3625\pi\text{m}^2\text{ of grass}\end{aligned}$ Now we know the area of grass the cow can eat, we can move on to the next step. We will let $G_n$ be the amount of grass on the $n$ th morning. Each day, we subtract $500\text{m}^2$ of grass, then multiply by $1.01$ for the grass regrowing by $1\%$ : $\begin{aligned}G_1&=3625\pi\\\\ G_2&=\left[G_1-500\right]\times1.01\\ &=\left[3625\pi-500\right]\times1.01\\ &=3625\pi(1.01)-500(1.01)\\\\ G_3&=\left[G_2-500\right]\times1.01\\ &=\left[3625\pi(1.01)-500(1.01)-500\right]\times1.01\\ &=3625\pi(1.01)^2-500\left(1.01+1.01^2\right)\\\\ G_4&=\left[G_3-500\right]\times1.01\\ &=\left[3625\pi(1.01)^2-500\left(1.01+1.01^2\right)-500\right]\times1.01\\ &=3625\pi(1.01)^3-500\left(1.01+1.01^2+1.01^3\right)\end{aligned}$ At this point we can see a pattern emerging, which we can generalise: $G_n=3625\pi(1.01)^{n-1}-500\left(1.01+1.01^2+1.01^3+\dots+1.01^{n-1}\right)$ Now we can use the formula for the sum of a geometric series. In this case, the first term $a$ is $1.01$ and the common ratio $r$ is also $1.01$ . $S_n=\frac{a\left(r^n-1\right)}{r-1}$ $\begin{aligned}G_n&=3625\pi(1.01)^{n-1}-500\left(1.01+1.01^2+1.01^3+\dots+1.01^{n-1}\right)\\ &=3625\pi(1.01)^{n-1}-500\left[\frac{1.01\left(1.01^{n-1}-1\right)}{0.01}\right]\\ &=3625\pi(1.01)^{n-1}-50500(1.01)^{n-1}+50500\\ &=(3625\pi-50500)(1.01)^{n-1}+50500\\\end{aligned}$ We are looking for the point where the cow does not have enough grass to eat, i.e. the amount of grass is less than $500\text{m}^2$ , so we will let $G_n$ equal $500$ and see what value of $n$ works. $\begin{aligned}G_n&=500\\ (3625\pi-50500)(1.01)^{n-1}+50500&=500\\ (1.01)^n&=\frac{-50000}{3625\pi-50500}\\ &\approx1.2784\\ \log(1.01)^n&=\log1.2784\\ n\log1.01&=\log1.2784\\ n&=\frac{\log1.2784}{\log1.01}\\ &\approx25.6827\end{aligned}$ This means that at some time between day $25$ and day $26$ , the amount of grass drops below $500$ . Therefore, the cow will not have enough grass to eat on day $\boxed{26}$