Choose any point of this hyperbola
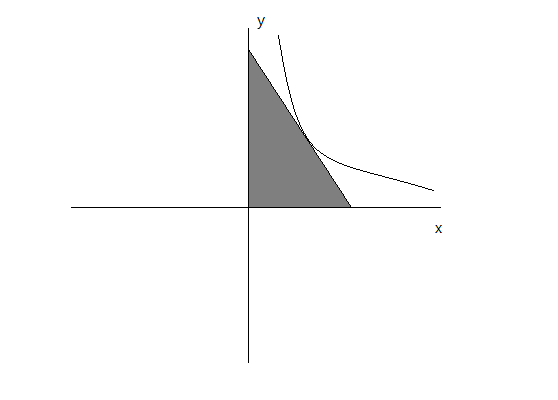
What is the area of the triangle delimited by any line tangent to the hyperbola and the coordinate axes?
Note.- My apologies for the picture.
Assumption.- the tangent line to the hyperbola passes through any point of the hyperbola
The answer is 4036.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let y = x 2 0 1 8 be our hyperbola in question whose derivative equals y ′ = − x 2 2 0 1 8 . Let P ( x 0 , x 0 2 0 1 8 ) , where x 0 > 0 , be any point on the hyperbola where the tangent line is expressible as:
y − x 0 2 0 1 8 = − x 0 2 2 0 1 8 ( x − x 0 ) ⇒ y = − x 0 2 2 0 1 8 x + x 0 4 0 3 6 (i).
Solving for the x and y-intercepts of this tangent line gives ( x , y ) = ( 2 x 0 , 0 ) ; ( 0 , x 0 4 0 3 6 ) , and the area of the right triangle contained between the coordinate axes + the tangent line equals:
A = 2 1 ⋅ ( 2 x 0 ) ( x 0 4 0 3 6 ) = 4 0 3 6 .