Choose Your Own Möbius Adventure — Part I

Geometry Level 2

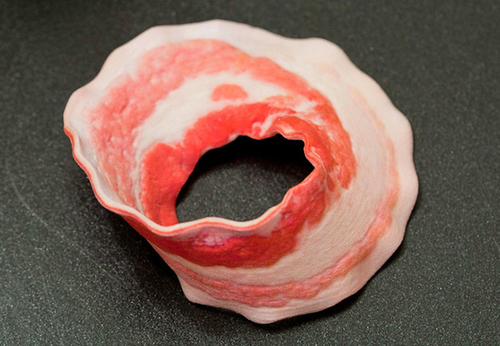A Möbius strip is formed by creating a ring with a single half-twist from a flat band.

How many sides does a Möbius strip possess?

Image credit: joabaldwin

Details and assumptions

This problem is part of the Choose Your Own Möbius Adventure series.

1 2 3 0

View wiki
Arron Kau by Arron Kau

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

9 solutions

Finn Hulse
Jan 24, 2014

The Mobius Strip only has 1 side! It's a paradox, because if you travel along one side, you will end up on the "other". Of course, it's actually the same side! IT'S MADNESS!!

49 Helpful 0 Interesting 0 Brilliant 0 Confused

Well said, Finn. :)

Arron Kau Staff - 7 years, 4 months ago

Log in to reply

Thanks!

Finn Hulse - 7 years, 3 months ago

Cool.

Soham Dibyachintan - 7 years, 4 months ago

now I know, thanks. :D

Patricia Ann Buiser - 7 years, 4 months ago

Log in to reply

u used to play our world, dont you ?

Shahan Shaikh - 7 years, 3 months ago

Mobius' loop is actually formed by merging the inner surface of the strip and its outer surface. Thus, instead of a half fold, if you fold it 1.5 times, 2.5 times, 3.5 times and so on, you will achieve the same result. Since the two surfaces are merged, the actual distance covered is TWICE the strip's length, because of the two combined sides...

Aditya De Saha - 7 years, 2 months ago

this is really great..

Shweta Iyer - 7 years, 4 months ago

this is awesome.

Akshay Gupta - 7 years, 4 months ago

oh yes

Saba Majeed - 7 years, 4 months ago

yes yes....

Jedhidya Katru - 7 years, 4 months ago

yes ot has a unique mathematical property of possesing one side

Siddharth Singh - 7 years, 3 months ago

It is just crazy :D

Amr Khaled - 7 years, 3 months ago

Paradox! It's scary!

Carlos E. C. do Nascimento - 7 years, 3 months ago

Cannot unsee

Alphonso Lopez - 7 years, 3 months ago

thats it

Lalyn Alagos - 7 years, 2 months ago

Strange and uncommon

Platinum Grieger - 7 years ago

Prove all angles of a triangle is greater than 180 degrees could. how?

mahla salarmohammadi - 4 years, 7 months ago
Gaurav Kadian
Jan 25, 2014

Just start with an imaginary point on the strip and start moving it on the strip. We will see that it comes to the same initial point without any break in the motion. Thus it is having only one side.

11 Helpful 0 Interesting 0 Brilliant 0 Confused

consider original rectangle from which it is made it has two side because of above reason

Aamir Faisal Ansari - 7 years, 4 months ago

Prove all angles of a triangle is greater than 180 degrees could. how?

mahla salarmohammadi - 4 years, 7 months ago
Swagat Suvankar
Feb 14, 2014

one surface

1 Helpful 0 Interesting 1 Brilliant 0 Confused
Paul Couch
Jan 27, 2014

I know this from a book I read.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

What book was it?

Solomon Lo - 7 years, 3 months ago
Ahaan Rungta
Feb 2, 2014

It only has one side . Draw a line in the middle, and pull the strip along as you draw; we arrive at the beginning of the line again without turning the paper over.

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Tin Long
Aug 14, 2020

A Möbius strip is made by having 1 strip of paper and twisting it 180 degrees then glueing them together (also a half-twist). If you have a pen and draw a line around it you will arrive back at where you started. Therefore, it only has 1 side.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Raven Herd
Jul 4, 2015

Please someone tell me more about these strips.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

As I put it it is a tantalizing paradoxical geometrical paradox

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Anubhav Balodhi
Jan 29, 2014

As simple as ever...

0 Helpful 0 Interesting 0 Brilliant 0 Confused

what about the edge of the strip isn't that also a side?

Johnny Driscoll - 7 years, 3 months ago

Log in to reply

yes.. it's considered as also having only one edge..

Agung Saptoko - 5 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...