Chopping Down A Tree

A perfectly symmetrical tree has a trunk in the shape of a cylinder with diameter 0 . 2 m . Since the tree is symmetrical the center of mass is at some distance L above the ground along the axis of the cylinder. A rotten lumberjack with no concept that he's cutting down the most amazing tree ever grown uses a chain saw to cut the tree down. He saws horizontally right at the base of the tree (ground level).
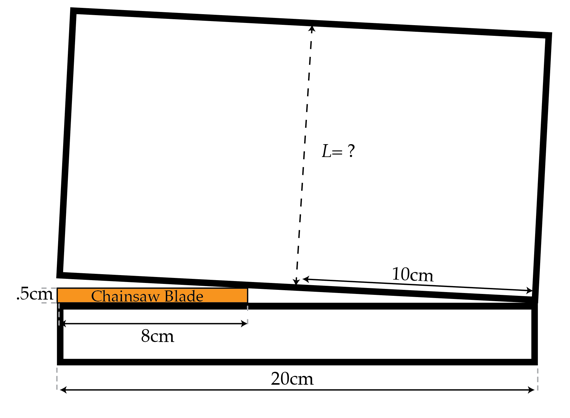
What is the minimum value of L in meters such that the tree begins to topple over as soon once the chain saw reaches the position in the picture?
Details and assumptions
- The chain saw blade is 8 cm wide and 0 . 5 cm high.
- Treat the tree as a rigid body.
The answer is 2.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
i did it same way
The tree begins to topple when the center of mass is not aligned vertically on the base of the tree. The critical angle θ c r i t is the angle in which toppling hapens. To find the critical angle, extend an imaginary line vertically upwards from the outermost part of the base, until it intersects the axis of the tree trunk. The intersection point forms a right triangle with the base's right side and the midpoint of the top cut of the base. Let the angle formed by the cut be θ The angle of inclination of the tree trunk is also equivalent to θ . Applying geometry concepts, we find that θ c r i t = θ , hence, the right triangle formed between the cut and the edge of the chainsaw blade is similar to the right triangle formed earlier, with θ c r i t as one of its angles. We treat L m i n as the length of the latter triangle's legs. Solving for the ratio 0 . 5 : 1 2 = 1 0 : L m i n , from the similar triangles proportion, we arrive with L m i n = 2 4 0 c m = 2 . 4 m .
My solution :
The angle of rotation is arctan(5/12). We just keep it as 5/12 The coordinates of original Center of mass = (10, L) Using the formulae for rotation, x2 = x1cos(theta) - y1 sin(theta) , we get x2 = 10 + L tan(theta) [dividing by cos(theta) and also using the fact that it is a clockwise rotation and sin(-theta) = -sin(theta)
x2 = 10 + L*5/12
Now the condition for toppling over is 10 + 5L / 12 >= 20 (the length of the base)
Looking at the point of equality as the critical point,
120 + 5L = 240
5L = 120
L = 24 cm
I forgot to convert to meters
But i think though the change in Y has not been incorporated, things become unstable pretty soon as Y increases and hence x will increase even further
Very nice question
I love this question !
The L you calculated is only half the length ? The CG is at half the length ?
that is the critical angle, because, then, the torque produced by the weight of the tree will cause it to topple to the right instead of the left. (about the point of contact of the trunk and the base)
The image below shows the limiting case
Torque about the vertex which contains θ is zero.
So, m g c o s ( θ ) × 1 0 = m g s i n ( θ ) × L ⟹ t a n ( θ ) = L 1 0 = 1 2 0 . 5 ⟹ L = 2 4 0 c m = 2 . 4 m