Chopping Up the Cube

The red prisms represent the combination of 3 pyramids, whereas the green prism represents the inner cube.

The sliced solid consists of 6 square pyramids and a cube of same square bases. Since the volume of the pyramid is $\frac{1}{3}$ the product of the square base area and the height, we can combine all six pyramids to form two combined rectangular prisms each with same height as the pyramid and same base. So the volume of the sliced polyhedron is the combined volume of two prisms and a cube (becoming a large rectangular prism), where

• The height of the prism is simply the longest distance between two opposite apex points which is $\frac{1}{2}$ times length of the large cube. Since the cutting plane slopes are linear, then the apex point of the pyramid is $\frac{1}{4}$ of the cube side length away from the closest square base.
• The length of the square base is $\frac{1}{3}$ the length of the large cube. This can be derived by observing the segments within the midsection passing through the apex point as shown below.

$J$ is the apex point, and segment $\overline{MN}$ corresponds to the segment of the base.

Thus, the volume ratio is the product of the three factors, which gives $\begin{array}{rl} V_P&= \text{base area factor} \times \text{height factor} \times V \\ &= \left(\dfrac{1}{3}\cdot\dfrac{1}{3}\cdot\dfrac{1}{2}\right)V=\dfrac{1}{18}V \end{array}$ where $\boxed{n=18}$ .

As the figure of the core shows, the faces of the core polyhedron are symmetrical with respect to the x, y, and z directions. The faces (hedrons) of the core are all congruent triangles symmetrical about the center of the cube. We need only find the vertices of one such triangle. Let the cube be centered at the origin with side length = 2.

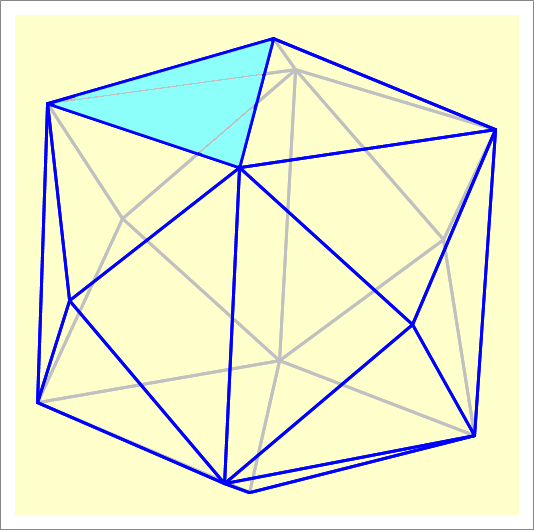
Consider the shaded triangle, the top vertex is the intersection of the following three planes

$(0, -1, 2) \cdot (r - (1,1,1)) = 0$

$(0, 1, 2) \cdot (r - (-1, -1, 1) ) = 0$

$(-1, 0, 2) \cdot (r - (1, 1, 1) ) = 0$

solving this linear system for r, we obtain

$r_1 = (0, 0, 0.5)$

the second vertex is the intersection of

$(0, -1, 2) \cdot (r - (1,1,1)) = 0$

$(1, 0, 2) \cdot (r - (-1, -1, 1) ) = 0$

$(0, -2, 1) \cdot (r - (-1, -1, -1) ) = 0$

solving again, results in

$r_2 = (1/3, -1/3, 1/3)$

so by symmetry the third vertex is at $r_3 = (-1/3, -1/3, 1/3)$

We're almost there. The next step is to compute the area of this triangle using cross product.

$\begin{aligned} \text{Area} &= 1/2 | (r_3 - r_1) \times (r_2 - r_1) | \\ &= 1/2 | (-1/3, -1/3, -1/6) \times (1/3, -1/3, -1/6) | \\ & = 1/2 | (0, -1/9, 2/9 ) | = \dfrac{1}{18} \sqrt{5} \\ \end{aligned}$

Next, the orthogonal distance from the center of the cube to the plane of the triangle is the projection of $(r_1 - r_C)$ onto the normal to the plane which we just computed.

$r_1 - r_C = r_1 = (0,0, 0.5)$

$h =| (0, 0, 0.5) \cdot ( 0, -1/9 , 2/9 ) / | (0, -1/9, 2/9) |$

$h = \dfrac{1/9 }{ (1/9) \sqrt{5} }= \dfrac{1}{ \sqrt{5}}$

Thus the volume of the small pyramid extending from the center of the core to the triangle is $V_1 = 1/3 A h = 1/3 (1/18)$

Hence, the total volume of the core is $V_P = 24 \cdot V_1 = (24/3) (1/18) = \dfrac{8}{18}$

The volume of the cube we started with is $V = 2^3 = 8$

Hence the ratio of the volumes is $\dfrac{1}{18}$ . Therefore, $n = 18$ .