Chord Circle Triad
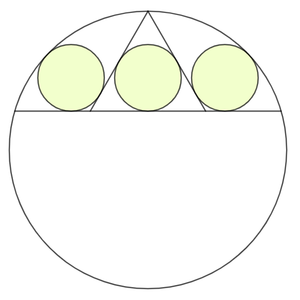
In the large circle, one of the three green circles of identical radii is the incircle of the equilateral triangle whose side length is , whereas two other circles are tangent to the chord and its circumference.
Determine the radius of the large circle.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Label the triangle A B C , the chord D E , A L be the median of △ A B C , the centers of the big circle, the middle green circle, and the right green circle be O , P , and Q , Q M perpendicular to D E , and the tangent point of the right green circle and the big circle be N . Note that O , Q , and N are colinear.
Let the radius of the green circles be r and that of the big circle be R . The median of △ A B C , A L = 1 2 3 sin 6 0 ∘ = 1 8 . Note that center P is the centroid of △ A B C . Therefore r = 3 1 ⋅ 1 8 = 6 .
By Pythagorean theorem :
O Q 2 − O P 2 ( O N − N Q ) 2 − ( O A − A P ) 2 ( O N − N Q ) 2 − ( O A − ( A L − P L ) ) 2 ( R − r ) 2 − ( R − 1 8 + r ) 2 ( R − 6 ) 2 − ( R − 1 2 ) 2 1 2 R − 1 0 8 ⟹ R = P Q 2 = ( L C + C M ) 2 = ( L C + Q M cot 6 0 ∘ ) 2 = ( 6 3 + 3 r ) = ( 6 3 + 2 3 ) 2 = 1 9 2 = 1 2 3 0 0 = 2 5