Chord in Motion while Confined in Semicircle

Geometry Level 4

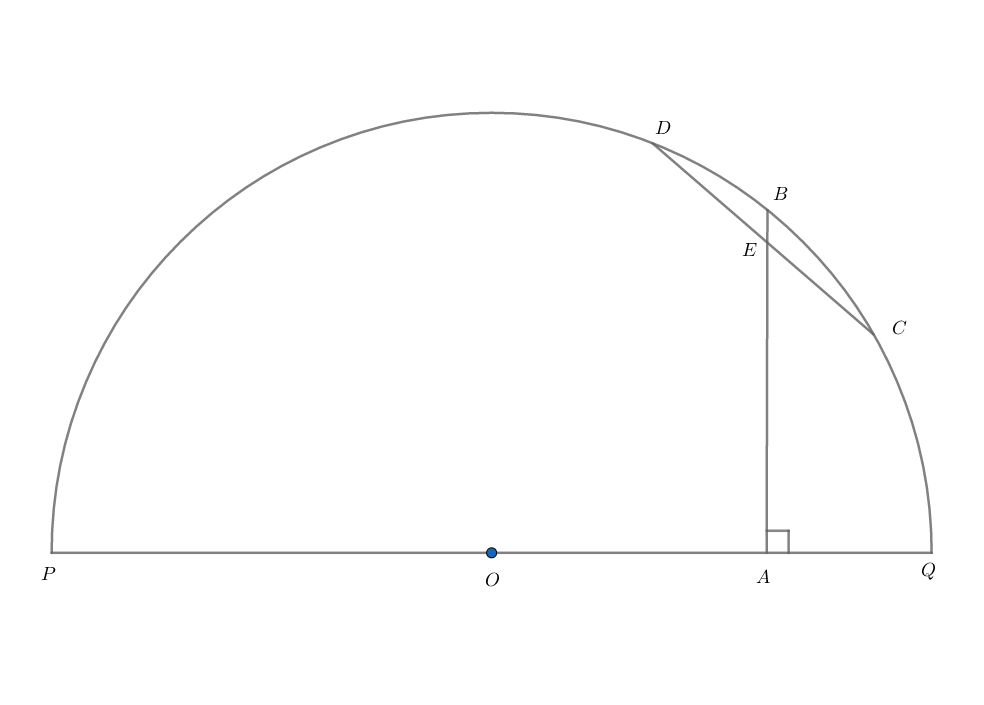
Here:

$PDQ$ is a semicircle with center at $O$ and diameter $PQ=100$ .
$B$ is a point on semicircle and $A$ is a point on diameter that $AB=14$ and $AB \perp PQ$ .
$CD$ is a chord that completely lies in the semicircle while its midpoint $E$ is a point between $A$ and $B$ .

Now:

$\alpha$ is the minimum possible value of $AE$ .
$\beta$ is the maximum possible value of $CD$ .
$\gamma$ is the minimum possible value of the acute angle between $AB$ and $CD$ .

The sum $(\alpha + \beta + \csc \gamma)$ can be expressed as $a+b\sqrt{c}$ , where each of $a$ , $b$ and $c$ is positive integers and $c$ is square-free.

Find the value of $a(b+c)$ .

The answer is 250.

1 solution

Jeremy Galvagni
Nov 3, 2018

As $AB$ is the geometric mean of $PA$ and $AQ$ , we can easily find $OA=48$ and $AQ=2$ .

The perpendicular bisector of a chord contains the center of a circle, so $\angle OEC=90$ .

All three conditions for $\alpha$ , $\beta$ , and $\gamma$ are met when $C=Q$ . (Which is rather boring in my opinion, but it does make the problem easier.)

When we do this, $AE$ becomes the geometric mean of $48$ and $2$ so $AE=\sqrt{96}$ or $\alpha=4\sqrt{6}$

We can then use the Pythagorean theorem on $\triangle AEC$ to find $CE=10$ or $CD=\beta =20$

Also, $\csc{\gamma}=\frac{BC}{AC}=5$

The sum is $25+4\sqrt{6}$ so $a=25$ , $b=4$ , and $c=6$ and the final answer is $25(4+6)=\boxed{250}$

Chord in Motion while Confined in Semicircle

The answer is 250.

1 solution

0 pending reports